��Ŀ����
2���ھ���ABCD�У�AB=6��AD=8����E��AB�ϣ���BE=2��P��BC�ϵĶ��㣨BP��2$\sqrt{3}$��������EP�����߶�EP�Ƶ�E��ʱ����תһ���ǶȺ�P����AD�ϵĵ�F������EP��EFΪ�ڱ���ƽ���ı���EPGF����1����ͼ1����BP=4ʱ����֤���ı���EPGF�������Σ�
��2����ͼ2����BP=6ʱ������G��GH��AD����AD���ӳ����ڵ�H������DG��FP��
�����ı���EPGF���ܳ���
����ֱ��д����EFP����BPF����HFG֮���������ϵ��
�����DFG�������
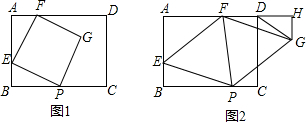
���� ��1����֤���ı���EFGP�����Σ���֤��$��\\;��$��FEP=90�㼴�ɣ�
��2������Rt��PBE�У����PE���ɽ�����⣮
�ڽ��ۣ���EFP=��BPF-��HFG������ƽ���ߵ������Լ����ε����ʼ���֤����
�����DF��GH������S ��DFG=$\frac{1}{2}$•FD•GH���㼴�ɣ�
��� ��1��֤������ͼ1�У�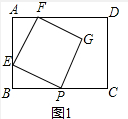
���ı���EPGF��ƽ���ı��Σ�
�֡�EF=EP��
��EPGF������
���ı���ABCD�Ǿ��Σ�
���A=��B=90�㣬
��AB=6��EB=2��
��AE=PB=4��
��Rt��AEF��Rt��BPE��
$\left\{\begin{array}{l}{AE=PB}\\{EF=EP}\end{array}\right.$
��Rt��AEF��Rt��BPE
��AEF=��BPE��
�ߡ�BPE+��BEP=90��
���AEF+��BEP=90��
���FEP=90��
��EPGF��������
��2����ͼ2�У�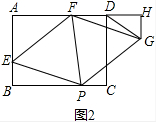
�ٽ⣺��Rt��PBE�У���BE=2 BP=6��
��EP=$\sqrt{B{E}^{2}+P{B}^{2}}$=2$\sqrt{10}$��
��EPGF������
���ı���EPGF���ܳ�Ϊ8$\sqrt{10}$��
�ڽ��ۣ���EFP=��BPF-��HFG��
���ɣ���AD��BC��
���HFP=��BPF��
���ı���EFGP�����Σ�
���EFP=��GFP=��FPE=��FPG��
���BPE=��HFG��
���BPF-��BPE=��EPF��
���BPF-��HFG=��EFP��
�۽⣺�ڡ�HFG�͡�PBE�У�
$\left\{\begin{array}{l}{��HFG=��BPE}\\{��H=��B=90��}\\{FG=PE}\end{array}\right.$
���HFG�ա�BPE��
��HG=BE=2��
��EF=EP=2$\sqrt{10}$��AE=4��
��AF=$\sqrt{��2\sqrt{10}��^{2}-{4}^{2}}$=2$\sqrt{6}$��
��FD=8-2$\sqrt{6}$��
��S ��DFG=$\frac{1}{2}$•FD•GH=$\frac{1}{2}$����8-2$\sqrt{6}$����2=8-2$\sqrt{6}$��
���� ���⿼���ı����ۺ��⡢���ε����ʡ����ε��ж������ʡ�ȫ�������ε��ж������ʡ����ɶ�����֪ʶ������Ĺؼ������������Щ֪ʶ������⣬�����п��������ͣ�

| A�� | 2017 | B�� | -2017 | C�� | $\frac{1}{2017}$ | D�� | -$\frac{1}{2017}$ |

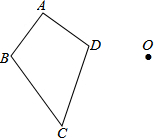 �Ե�OΪλ�����ģ������ı���ABCD��λ��ͼ�Σ�ʹ������ͼ����ԭͼ�ε�λ�Ʊ�Ϊ2��1��
�Ե�OΪλ�����ģ������ı���ABCD��λ��ͼ�Σ�ʹ������ͼ����ԭͼ�ε�λ�Ʊ�Ϊ2��1��