题目内容
12.(1)参加一次聚会的每两人都握了一次手,所有人共握手66次,有多少人参加聚会?(2)要组织一场篮球联赛,赛制为单循环形式,即每两队之间都赛一场,计划安排28场比赛,应邀请多少个球队参加比赛?
(3)初三毕业晚会时每人互相送照片一张,一共要90张照片,有多少人?
(注:3个小题只需设未知数,列出方程即可)
分析 (1)先设有x人参加聚会,根据每两人都握手一次手,有人共握手66次,列出代数式,求出x的值,再根据x只能取正数,即可得出答案
(2)设邀请x个球队参加比赛,那么第一个球队和其他球队打(x-1)场球,第二个球队和其他球队打(x-2)场,以此类推可以知道共打(1+2+3+…+x-1)场球,然后根据计划安排28场比赛即可列出方程求解;
(3)设有学生x人,由每人都向其他同学赠送一张可知,每人赠出的卡片为(x-1)张,则x(x-1)=90.
解答 解:(1)设有x人参加聚会,
根据题意得:$\frac{x(x-1)}{2}$=66;
(2)设共有x个队参赛,
由题意得:$\frac{1}{2}$x(x-1)=28;
(3)解:设共有学生x人.
则x(x-1)=90.
点评 此题主要考查了一元一次方程的应用,准确找到关键描述语,从而根据等量关系准确的列出方程是解决问题的关键.

练习册系列答案
相关题目
3.正整数按如图的规律排列,请写出第15行,第17列的数字是( )


| A. | 271 | B. | 270 | C. | 256 | D. | 255 |
7.设点A(x1,y1)和点B(x2,y2)是反比例函数y=$\frac{k}{x}$图象上的两点,当x1<x2<0时,y1>y2,则一次函数y=-2x+k的图象不经过的象限是( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
5.下列运算有错误的是( )
| A. | $\frac{1}{3}$÷(-3)=3×(-3) | B. | (-5)÷(-$\frac{1}{2}$)=-5×(-2) | C. | 5-(-2)=5+2 | D. | 2-3=(+2)+(-3) |
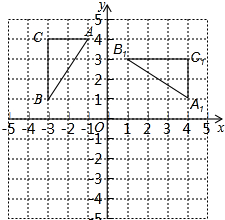 如图,在平面直角坐标系中,△ABC三个顶点分别为A(-1,4)、B(-3,1)、C(-3、4),△A1B1C1是由△ABC绕某一点顺时针旋转得到的.
如图,在平面直角坐标系中,△ABC三个顶点分别为A(-1,4)、B(-3,1)、C(-3、4),△A1B1C1是由△ABC绕某一点顺时针旋转得到的.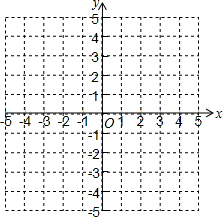 如图,在平面直角坐标系xOy中,已知点P(-1,0),C($\sqrt{2}$-1,1),D(0,-3),A,B在x轴上,且P为AB中点,S△CAP=1.
如图,在平面直角坐标系xOy中,已知点P(-1,0),C($\sqrt{2}$-1,1),D(0,-3),A,B在x轴上,且P为AB中点,S△CAP=1.