题目内容
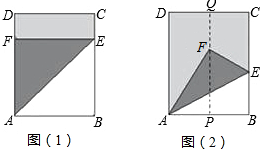 在一张长方形纸片ABCD中,AD=5cm,AB=4cm,现将这张纸片按图示方式折叠,请分别求出折痕的长.
在一张长方形纸片ABCD中,AD=5cm,AB=4cm,现将这张纸片按图示方式折叠,请分别求出折痕的长.(1)如图(1),B点落在AD上的点F处,折痕为AE;
(2)如图(2),P、Q分别为AB、CD的中点,B点落在PQ上的点F处,折痕为AE.
考点:翻折变换(折叠问题)
专题:
分析:(1)如图1,证明∠EAB=∠AEB=45°,得到AB=BE=4;由勾股定理即可解决问题.
(2)如图2,证明AD∥PQ∥BC,得到AG=GE,∠DAF=∠AFG;证明∠DAF=∠FAG=∠EAB=30°,借助边角关系即可解决问题.
(2)如图2,证明AD∥PQ∥BC,得到AG=GE,∠DAF=∠AFG;证明∠DAF=∠FAG=∠EAB=30°,借助边角关系即可解决问题.
解答: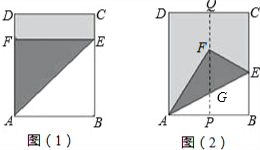 解:(1)如图(1),由题意得:
解:(1)如图(1),由题意得:
∠FAE=∠BAE;
∵四边形ABCD为矩形,
∴∠FAB=∠B=90°,
∴∠EAB=∠AEB=45°,
∴AB=BE=4,
由勾股定理得:AE2=42+42,
∴AE=4
(cm).
(2)∵四边形ABCD是矩形,且P、Q分别是AB、CD的中点,
∴AD∥PQ∥BC,而DQ=CQ,
∴AG=GE;∠DAF=∠AFG;
由题意得:∠AFE=∠B=90°,∠FAG=∠BAE;
∵FG是直角△AFE的斜边上的中线,
∴FG=AG,∠AFG=∠FAG;
∴∠DAF=∠FAG=∠EAB=30°,
∵cos30°=
,
∴AE=
(cm).
 解:(1)如图(1),由题意得:
解:(1)如图(1),由题意得:∠FAE=∠BAE;
∵四边形ABCD为矩形,
∴∠FAB=∠B=90°,
∴∠EAB=∠AEB=45°,
∴AB=BE=4,
由勾股定理得:AE2=42+42,
∴AE=4
| 2 |
(2)∵四边形ABCD是矩形,且P、Q分别是AB、CD的中点,
∴AD∥PQ∥BC,而DQ=CQ,
∴AG=GE;∠DAF=∠AFG;
由题意得:∠AFE=∠B=90°,∠FAG=∠BAE;
∵FG是直角△AFE的斜边上的中线,
∴FG=AG,∠AFG=∠FAG;
∴∠DAF=∠FAG=∠EAB=30°,
∵cos30°=
| AB |
| AE |
∴AE=
8
| ||
| 3 |
点评:该题主要考查了翻折变换的性质及其应用问题;解题的关键是牢固掌握矩形的性质、翻折变换的性质等几何知识点,灵活运用有关定理来解题.

练习册系列答案
 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
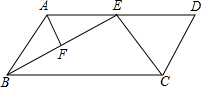 如图,AB∥CD,BC∥AD,BE、CE分别是∠ABC、∠BCD的平分线,F是BE的中点.
如图,AB∥CD,BC∥AD,BE、CE分别是∠ABC、∠BCD的平分线,F是BE的中点.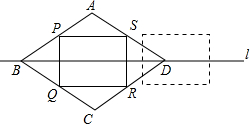 在菱形ABCD中,AB=5cm,BD=8cm,P,Q,R,S分别是菱形各边的中点.将长方形PQRS沿着直线L向右移动5cm,则长方形PQRS与菱形ABCD重叠的面积是多少?
在菱形ABCD中,AB=5cm,BD=8cm,P,Q,R,S分别是菱形各边的中点.将长方形PQRS沿着直线L向右移动5cm,则长方形PQRS与菱形ABCD重叠的面积是多少?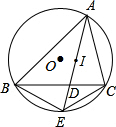 如图,△ABC内接于⊙O,I是△ABC的内心,AI交BC于点D,交⊙O于点E,试说明BE、CE、IE的大小关系.
如图,△ABC内接于⊙O,I是△ABC的内心,AI交BC于点D,交⊙O于点E,试说明BE、CE、IE的大小关系.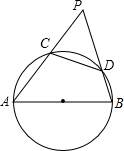 如图,已知圆的直径,AB=6cm,CD是圆上长为2cm的弦,当弦CD在半圆AB上滑动时,AC和BD延长线的夹角是否为定值?如果不是,说明理由;如果是,求出这个定角的正弦值.
如图,已知圆的直径,AB=6cm,CD是圆上长为2cm的弦,当弦CD在半圆AB上滑动时,AC和BD延长线的夹角是否为定值?如果不是,说明理由;如果是,求出这个定角的正弦值.