题目内容
如图,已知∠AOC与∠BOD具有公用顶点,∠COD是两个角叠合的部分.
(1)观察图1:若∠AOC=∠BOD=90°,完成下列问题:
①直接写出图中两个相等的锐角: = ;②若∠COD=40°,则∠AOB= ,③若∠AOB=150°,则∠COD= ;④猜想∠AOB+∠DOC= .请说明理由.
(2)探究如图2:完成下列问题:
①若∠AOC=60°,∠BOD=50°,②则∠AOB+∠DOC= ;③若∠AOC=α,∠BOD=β,④则∠AOB+∠DOC= ,请说明理由.

(1)观察图1:若∠AOC=∠BOD=90°,完成下列问题:
①直接写出图中两个相等的锐角:
(2)探究如图2:完成下列问题:
①若∠AOC=60°,∠BOD=50°,②则∠AOB+∠DOC=

考点:余角和补角,角的计算
专题:
分析:(1)①利用等角的余角相等得出答案即可;
②③④利用余角的意义和角的和与差计算即可;
(2)②④利用角的和与差计算即可.
②③④利用余角的意义和角的和与差计算即可;
(2)②④利用角的和与差计算即可.
解答:解:(1)①若∠AOC=∠BOD=90°,
∠AOD+∠COD=∠BOC+∠COD=90°,
∴∠AOD=∠BOC;
②∵∠COD=40°,
∴∠AOD=50°,
∠AOB=∠AOD+∠BOD=140°,
③若∠AOB=150°,则∠AOD=∠AOB-90°=60°,
∴∠COD=90°-∠AOD=30°.
④∠AOB+∠DOC=90°+∠AOD+∠DOC=90°+90°=180°.
(2)②若∠AOC=60°,∠BOD=50°,
则∠AOB+∠DOC=∠AOD+∠DOC+∠BOC+∠DOC=∠AOC+∠BOD=110°.
④若∠AOC=α,∠BOD=β,则∠AOB+∠DOC=∠AOD+∠DOC+∠BOC+∠DOC=∠AOC+∠BOD=α+β.
故答案为:(1)①∠AOD,∠BOC;②140°.③30°.④180°;(2)②110°,④α+β.
∠AOD+∠COD=∠BOC+∠COD=90°,
∴∠AOD=∠BOC;
②∵∠COD=40°,
∴∠AOD=50°,
∠AOB=∠AOD+∠BOD=140°,
③若∠AOB=150°,则∠AOD=∠AOB-90°=60°,
∴∠COD=90°-∠AOD=30°.
④∠AOB+∠DOC=90°+∠AOD+∠DOC=90°+90°=180°.
(2)②若∠AOC=60°,∠BOD=50°,
则∠AOB+∠DOC=∠AOD+∠DOC+∠BOC+∠DOC=∠AOC+∠BOD=110°.
④若∠AOC=α,∠BOD=β,则∠AOB+∠DOC=∠AOD+∠DOC+∠BOC+∠DOC=∠AOC+∠BOD=α+β.
故答案为:(1)①∠AOD,∠BOC;②140°.③30°.④180°;(2)②110°,④α+β.
点评:此题考查了余角和补角以及角的计算等知识,角的和与差需要结合图形,灵活解答.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
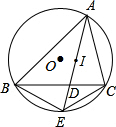 如图,△ABC内接于⊙O,I是△ABC的内心,AI交BC于点D,交⊙O于点E,试说明BE、CE、IE的大小关系.
如图,△ABC内接于⊙O,I是△ABC的内心,AI交BC于点D,交⊙O于点E,试说明BE、CE、IE的大小关系.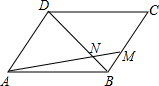 如图,在?ABCD中,M是边BC上的一点,AM与BD相交于点N,且AM:NM=4:1.
如图,在?ABCD中,M是边BC上的一点,AM与BD相交于点N,且AM:NM=4:1. 如图,点B、D、C是⊙A上的点,∠BDC=130°,则∠BAC=
如图,点B、D、C是⊙A上的点,∠BDC=130°,则∠BAC=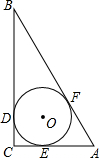 如图,在Rt△ABC中,∠C=90°,AC=5cm,BC=12cm.
如图,在Rt△ABC中,∠C=90°,AC=5cm,BC=12cm. 某小区有100个停车位,给业主停车带来了方便,去年1-6月,每个车位租价y为360元,7-12月,每个车位租价y(元)与月份x关系如表所示.去年1-12月,每月租出车位m(个)与月份x关系如图.已知业主只需支付月租给物管公司,公司每月每车位需支付管理费p=6x(1≤x≤12,x取整数).
某小区有100个停车位,给业主停车带来了方便,去年1-6月,每个车位租价y为360元,7-12月,每个车位租价y(元)与月份x关系如表所示.去年1-12月,每月租出车位m(个)与月份x关系如图.已知业主只需支付月租给物管公司,公司每月每车位需支付管理费p=6x(1≤x≤12,x取整数).