题目内容
12.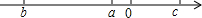 已知实数a、b、c在数轴上的位置如图所示,则化简$\sqrt{{a}^{2}}$-$\sqrt{(a-b)^{2}}$+$\sqrt{(a-c)^{2}}$+$\sqrt{(b+c)^{2}}$的结果是( )
已知实数a、b、c在数轴上的位置如图所示,则化简$\sqrt{{a}^{2}}$-$\sqrt{(a-b)^{2}}$+$\sqrt{(a-c)^{2}}$+$\sqrt{(b+c)^{2}}$的结果是( )| A. | -3a | B. | a+2b | C. | 2b | D. | a |
分析 根据数轴上点的坐标,可得a、b、c的关系,根据二次根式的性质,可化简二次根式,根据整式的加法,可得答案.
解答 解:由数轴上点的位置关系,得
b<a<0<c,|b|>|c|>|a|.
$\sqrt{{a}^{2}}$-$\sqrt{(a-b)^{2}}$+$\sqrt{(a-c)^{2}}$+$\sqrt{(b+c)^{2}}$
=-a-(a-b)+(c-a)+[-(b+c)]
=-a-a+b+c-a-b-c
=-3a.
故选:A.
点评 本题考查了实数与数轴,利用二次根式的性质化简二次根式是解题关键.

练习册系列答案
相关题目
20.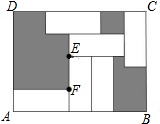 如图,长方形ABCD中有6个形状、大小相同的小长方形,且EF=3,CD=12,则大长方形ABCD的面积为( )
如图,长方形ABCD中有6个形状、大小相同的小长方形,且EF=3,CD=12,则大长方形ABCD的面积为( )
 如图,长方形ABCD中有6个形状、大小相同的小长方形,且EF=3,CD=12,则大长方形ABCD的面积为( )
如图,长方形ABCD中有6个形状、大小相同的小长方形,且EF=3,CD=12,则大长方形ABCD的面积为( )| A. | 105 | B. | 106 | C. | 107 | D. | 108 |
 如图,直线AB、CD交于点O,∠AOC:∠BOC=4:5,且OE⊥CD,则∠AOE=10度.
如图,直线AB、CD交于点O,∠AOC:∠BOC=4:5,且OE⊥CD,则∠AOE=10度. 用4个完全相同的小正方体组成如图所示的立体图形,它的主视图是( )
用4个完全相同的小正方体组成如图所示的立体图形,它的主视图是( )



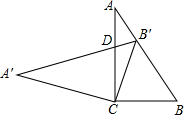 在Rt△ABC中,∠ACB=90°,cosB=$\frac{3}{5}$,将△ABC绕点C旋转后得到△A′B′C,其中B′点正好落在边AB上,A′B′交于点D,则$\frac{B′D}{CD}$的值为$\frac{7}{20}$.
在Rt△ABC中,∠ACB=90°,cosB=$\frac{3}{5}$,将△ABC绕点C旋转后得到△A′B′C,其中B′点正好落在边AB上,A′B′交于点D,则$\frac{B′D}{CD}$的值为$\frac{7}{20}$.