题目内容
6. 如图,在直角△ABC中,∠C=90°,∠CAB的平分线AD交BC于D,若DE⊥AB于点E,CD=3,AB=12,求△ABD的面积.
如图,在直角△ABC中,∠C=90°,∠CAB的平分线AD交BC于D,若DE⊥AB于点E,CD=3,AB=12,求△ABD的面积.
分析 根据角的平分线上的点到角的两边的距离相等得到DE=CD=3,根据三角形面积公式计算得到答案.
解答 解:∵AD是∠CAB的平分线,∠C=90°,DE⊥AB,
∴DE=CD=3,
∴△ABD的面积=$\frac{1}{2}$×AB×DE=18.
点评 本题考查的是角平分线的性质,掌握角的平分线上的点到角的两边的距离相等是解题的关键.

练习册系列答案
相关题目
17.在⊙O中,弦AB到圆心的距离为d1,在⊙O1中,弦CD到圆心的距离为d2,若d1=d2,则( )
| A. | AB>CD | B. | AB=CD | ||
| C. | AB<CD | D. | AB,CD的大小不确定 |
11.若a2-$\sqrt{22}$a+1=0,则a-$\frac{1}{a}$的值是( )
| A. | ±2$\sqrt{3}$ | B. | ±3$\sqrt{2}$ | C. | ±4$\sqrt{3}$ | D. | ±6$\sqrt{2}$ |
 =0,
=0, =-4,
=-4, =7,按此规律,
=7,按此规律, =-5.
=-5.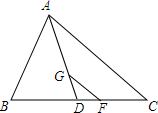 如图ABC中,G是重心,AG的延长线交BC于D,过点G作GF∥AC,交BC于F,则S△DGF:S△DAC=1:9.
如图ABC中,G是重心,AG的延长线交BC于D,过点G作GF∥AC,交BC于F,则S△DGF:S△DAC=1:9. 如图,已知l1,l2分别是△ABC的边AB、BC的垂直平分线,l1与l2相交于点O,试判断线段0A与OC的数量关系.
如图,已知l1,l2分别是△ABC的边AB、BC的垂直平分线,l1与l2相交于点O,试判断线段0A与OC的数量关系. 如图,已知,在△ABC中,CD⊥AB于点D,BE⊥AC于点E,连接DE.求证:
如图,已知,在△ABC中,CD⊥AB于点D,BE⊥AC于点E,连接DE.求证: