题目内容
16. 如图,已知,在△ABC中,CD⊥AB于点D,BE⊥AC于点E,连接DE.求证:
如图,已知,在△ABC中,CD⊥AB于点D,BE⊥AC于点E,连接DE.求证:(1)△ABE∽△ACD;
(2)△ABC∽△AED.
分析 (1)先利用垂直的定义得到∠ADC=∠AEB=90°,再加上公共角即可判断△ABE∽△ACD;
(2)利用△ABE∽△ACD得到$\frac{AB}{AC}$=$\frac{AE}{AD}$,则利用比例性质得$\frac{AD}{AC}$=$\frac{AE}{AB}$,加上公共角,于是可根据两组对应边的比相等且夹角对应相等的两个三角形相似得到结论.
解答 证明:(1)∵CD⊥AB于点D,BE⊥AC于点E,
∴∠ADC=∠AEB=90°,
∵∠BAE=∠CAD,
∴△ABE∽△ACD;
(2)∵△ABE∽△ACD,
∴$\frac{AB}{AC}$=$\frac{AE}{AD}$,
∴$\frac{AD}{AC}$=$\frac{AE}{AB}$,
∵∠DAE=∠CAB,
∴△ABC∽△AED.
点评 本题考查了相似三角形的判定:两组对应边的比相等且夹角对应相等的两个三角形相似;有两组角对应相等的两个三角形相似.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.用配方法解方程x2+2x+5=0时,原方程变形为( )
| A. | (x+1)2=6 | B. | (x+1)2+4=0 | C. | (x+2)2=9 | D. | (x+1)2=1 |
 如图,在直角△ABC中,∠C=90°,∠CAB的平分线AD交BC于D,若DE⊥AB于点E,CD=3,AB=12,求△ABD的面积.
如图,在直角△ABC中,∠C=90°,∠CAB的平分线AD交BC于D,若DE⊥AB于点E,CD=3,AB=12,求△ABD的面积. 如图,在△ABC中,∠CAD=∠ACD,若△ABD和△ABC的周长分别为24cm和37cm,求AC的长.
如图,在△ABC中,∠CAD=∠ACD,若△ABD和△ABC的周长分别为24cm和37cm,求AC的长.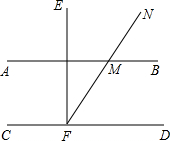 如图,AB∥CD,EF⊥CD于点F,射线FN交AB于点M,∠NMB=57°,则∠EFN=33°.
如图,AB∥CD,EF⊥CD于点F,射线FN交AB于点M,∠NMB=57°,则∠EFN=33°.