题目内容

1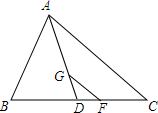．如图ABC中，G是重心，AG的延长线交BC于D，过点G作GF∥AC，交BC于F，则S△DGF：S△DAC=1：9．

分析 根据重心的性质得到$\frac{DG}{DA}$=$\frac{1}{3}$，根据相似三角形的面积比等于相似比的平方计算即可．

解答 解：∵G是重心，
∴$\frac{DG}{DA}$=$\frac{1}{3}$，
∵GF∥AC，
∴△GDF∽△ADC，
∴S△DGF：S△DAC=1：9，
故答案为：1：9．

点评 本题考查的是三角形的重心的概念和性质，掌握重心到顶点的距离是它到对边中点的距离的2倍是解题的关键，注意相似三角形的面积比等于相似比的平方．

练习册系列答案
相关题目
11．0的相反数是0；-（-$\frac{1}{5}$）的相反数是-$\frac{1}{5}$；-[+（-1）]的相反数是-1．
12．式子4+|x-1|能取得的最小值是4，这时x=1；式子3-|2x-1|能取得的最大值是3，这时x=0.5．
9．已知某山区海拔每升高1000米，气温大约降低6℃，某种植物适宜生长在温度为20℃的山坡上，现在测得山脚下的温度为23℃，那么该植物种在山的哪一部分为宜？
16．观察下列一组等式，然后解答后面的问题：
（$\sqrt{2}$+1）（$\sqrt{2}$-1）=1，（$\sqrt{3}$+$\sqrt{2}$）（$\sqrt{3}$$-\sqrt{2}$）=1，（$\sqrt{4}$+$\sqrt{3}$）（$\sqrt{4}$-$\sqrt{3}$）=1，（$\sqrt{5}$+$\sqrt{4}$）（$\sqrt{5}$-$\sqrt{4}$）=1，…（1）观察上面的规律，计算下列式子的值．
（$\frac{1}{\sqrt{2}+1}$$+\frac{1}{\sqrt{3}+\sqrt{2}}$$+\frac{1}{\sqrt{4}+\sqrt{3}}$+…+$\frac{1}{\sqrt{2016}+\sqrt{2015}}$）（$\sqrt{2016}$+1）
（2）利用上面的规律，试比较$\sqrt{12}$-$\sqrt{11}$与$\sqrt{13}$-$\sqrt{12}$的大小．
6．如图，在直角△ABC中，∠C=90°，∠CAB的平分线AD交BC于D，若DE⊥AB于点E，CD=3，AB=12，求△ABD的面积．
13．（x-y+z）（-x+y+z）=[z+（x-y）][z-（x-y）]=z2-（x-y）2．
10．等腰三角形的两内角的度数之比为1：4，则该三角形底边上的中线与腰的夹角为60°或10°．
11．用配方法解方程x2+2x+5=0时，原方程变形为（　　）
A．（x+1）2=6B．（x+1）2+4=0C．（x+2）2=9D．（x+1）2=1

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网