题目内容
9.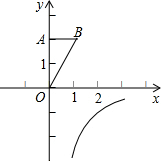 如图,OA在y轴上,点B在第一象限内,OA=2,OB=$\sqrt{5}$,若将△OAB绕点O顺时针方向旋转90°,此时点B恰好落在反比例函数y=$\frac{k}{x}$(x>0)的图象上,则该反比例函数的函数关系式是y=-$\frac{2}{x}$.
如图,OA在y轴上,点B在第一象限内,OA=2,OB=$\sqrt{5}$,若将△OAB绕点O顺时针方向旋转90°,此时点B恰好落在反比例函数y=$\frac{k}{x}$(x>0)的图象上,则该反比例函数的函数关系式是y=-$\frac{2}{x}$.
分析 利用勾股定理求出AB的长,作出图形,根据旋转变换只改变图形的位置不改变图形的形状与大小,可得OA′=OA,A′B′=AB,然后写出点B′的坐标,再利用待定系数法求反比例函数解析式解答.
解答 解:在Rt△OAB中,∵OA=2,OB=$\sqrt{5}$,
∴AB=$\sqrt{O{B}^{2}-O{A}^{2}}=\sqrt{(\sqrt{5})^{2}-{2}^{2}}$=1,
∵△OA′B′是Rt△OAB绕点O顺时针方向旋转90°得到,
∴OA′=OA=2,A′B′=AB=1,
∴点B′(2,-1),
∵点B′在反比例函数y=$\frac{k}{x}$(x>0)的图象上,
∴$\frac{k}{2}$=-1,
解得k=-2.
故答案为:y=-$\frac{2}{x}$.
点评 本题考查了坐标与图形变化-旋转,待定系数法求反比例函数解析式,利用旋转变换只改变图形的位置不改变图形的形状与大小,求出旋转后的点B的对应点的坐标是解题的关键.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
14.在三角形ABC中,BD是∠ABC的平分线,若∠A=60°,∠C=50°,则∠DBC=( )
| A. | 40度 | B. | 45度 | C. | 35度 | D. | 55度 |
19. 在?ABCD中,∠ACB=25°,现将?ABCD沿EF折叠,使点C与点A重合,点D落在G处,则∠GFE的度数( )
在?ABCD中,∠ACB=25°,现将?ABCD沿EF折叠,使点C与点A重合,点D落在G处,则∠GFE的度数( )
 在?ABCD中,∠ACB=25°,现将?ABCD沿EF折叠,使点C与点A重合,点D落在G处,则∠GFE的度数( )
在?ABCD中,∠ACB=25°,现将?ABCD沿EF折叠,使点C与点A重合,点D落在G处,则∠GFE的度数( )| A. | 135° | B. | 120° | C. | 115° | D. | 100° |

 如图,△ABC中,AB=AC,∠A=30°,DE垂直平分AC,求∠BCD.
如图,△ABC中,AB=AC,∠A=30°,DE垂直平分AC,求∠BCD.