题目内容
4．解不等式组$\left\{\begin{array}{l}{\frac{x-1}{3}+3≥-x+2}\\{3-2（x-2）＞1+x}\end{array}\right.$并将其解集在数轴上表示出来，同时写出不等式组的整数解．
分析 根据不等式的性质求出不等式的解集，根据找不等式组解集的规律找出即可．
解答 解：$\left\{\begin{array}{l}{\frac{x-1}{3}+3≥-x+2①}\\{3-2（x-2）＞1+x②}\end{array}\right.$，
解不等式①得：x≥-$\frac{1}{2}$，
解不等式②得：x＜2，
∴不等式组的解即是-$\frac{1}{2}$≤x＜2．
在数轴上表示不等式的解集为：
．
点评 本题考查了对不等式的性质，解一元一次不等式（组），在数轴上表示不等式组的解集等知识点的理解和掌握，关键是能根据不等式的解集找出不等式组的解集，题目比较典型，难度适中．
练习册系列答案
相关题目
12．下列方程中，是二元一次方程组的是（ ）
| A． | $\left\{\begin{array}{l}{3x-y=6}\\{xy=10}\end{array}\right.$ | B． | $\left\{\begin{array}{l}{\frac{x}{3}-\frac{y}{2}=1}\\{2x-3y=2}\end{array}\right.$ | C． | $\left\{\begin{array}{l}{\frac{5}{x}-y=6}\\{x+y=0}\end{array}\right.$ | D． | $\left\{\begin{array}{l}{x-2y=0}\\{y+z=1}\end{array}\right.$ |
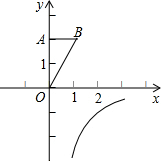如图，OA在y轴上，点B在第一象限内，OA=2，OB=$\sqrt{5}$，若将△OAB绕点O顺时针方向旋转90°，此时点B恰好落在反比例函数y=$\frac{k}{x}$（x＞0）的图象上，则该反比例函数的函数关系式是y=-$\frac{2}{x}$．
13．如果一次函数y=kx+b的图象经过第二象限内一点，且与y轴负半轴相交，那么（ ）
| A． | k＜0，b＜0 | B． | k＞0，b＜0 | C． | k＜0，b＞0 | D． | k＞0，b＞0 |
实数a、b、c在数轴上的位置如图所示，化简：$\sqrt{（a-b）^{2}}$-|a+c|+$\sqrt{（c-b）^{2}}$-|-2b|．