题目内容
16.对于抛物线y=5x2+l,有下列说法:①抛物线与y轴的交点坐标为(1,0);
②抛物线和x轴交于两点;
③将其向右平移2个单位.再向上平移3个单位.得到的抛物线是y=5(x+2)2+4;
④当x>0时,y随x的增大而增大.
其中正确的个数为( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 ①令x=0,可得y=1,可得抛物线与y轴的交点坐标为(0,1);
②根据抛物线交点个数与根的判别式的关系,求出△的值即可判断;
③根据平移的规律即可得到结果;
④根据二次函数的增减性可得结果.
解答 解:①令x=0,可得y=1,∴抛物线与y轴的交点坐标为(0,1),故本选项错误;
②∵a=5,b=0,c=1,
∴△=0-4×5×1=-20<0,
∴抛物线与x轴有无交点,故本选项错误;
③将其向右平移2个单位.再向上平移3个单位.得到的抛物线是y=5(x-2)2+4,故此选项错误;
④∵对称轴为:x=0,a=5>0,开口向上,
∴当x>0时,y随x的增大而增大,故此选项正确,
正确的选项共1个.
故选A.
点评 本题考查了二次函数的性质,牢记形如y=ax2+k的二次函数的性质是解答本题的关键.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
6.绝对值大于3且小于6的所有整数的和是( )
| A. | 0 | B. | 9 | C. | 6 | D. | 18 |
7.0.5097精确到千分位,正确的是( )
| A. | 0.5097≈0.510 | B. | 0.5097≈0.51 | C. | 0.5097≈0.500 | D. | 0.5097≈0.509 |
4.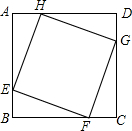 如图,正方形ABCD的边长为8,在各边上顺次截取AE=BF=CG=DH=5,则四边形EFGH的面积是( )
如图,正方形ABCD的边长为8,在各边上顺次截取AE=BF=CG=DH=5,则四边形EFGH的面积是( )
 如图,正方形ABCD的边长为8,在各边上顺次截取AE=BF=CG=DH=5,则四边形EFGH的面积是( )
如图,正方形ABCD的边长为8,在各边上顺次截取AE=BF=CG=DH=5,则四边形EFGH的面积是( )| A. | 30 | B. | 34 | C. | 36 | D. | 40 |
11.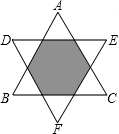 如图将正△ABC绕其中心至少旋转下列哪个角度才能得到另一个三角形( )
如图将正△ABC绕其中心至少旋转下列哪个角度才能得到另一个三角形( )
 如图将正△ABC绕其中心至少旋转下列哪个角度才能得到另一个三角形( )
如图将正△ABC绕其中心至少旋转下列哪个角度才能得到另一个三角形( )| A. | 30° | B. | 60° | C. | 90° | D. | 120° |
8.计算(m3n)2的结果是( )
| A. | m6 | B. | m6n2 | C. | m3n2 | D. | m5n2 |
6.如果把$\frac{2y}{2x-3y}$中的x和y都扩大10倍,那么分式的值( )
| A. | 不变 | B. | 扩大10倍 | C. | 缩小10倍 | D. | 扩大20倍 |
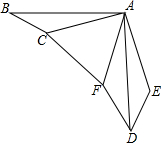 如图,在△ABC中,∠BAC=15°,将△ABC绕点A按逆时针方向旋转90°,到△ADE的位置,然后将△ADE以AD为轴翻折到△ADF的位置,连接CF,判断△ACF的形状,并说明理由.
如图,在△ABC中,∠BAC=15°,将△ABC绕点A按逆时针方向旋转90°,到△ADE的位置,然后将△ADE以AD为轴翻折到△ADF的位置,连接CF,判断△ACF的形状,并说明理由.