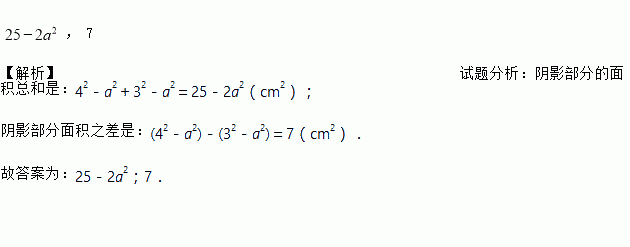题目内容
如图，两个边长分别为4cm与3cm的正方形的一部分重叠在一起，重叠部分是边长为acm的正方形，则图中阴影部分的面积总和是_____cm2．面积之差是_____cm2
， 7
【解析】试题分析：阴影部分的面积总和是：42－a2＋32－a2＝25－2a2（cm2）；
阴影部分面积之差是：(42－a2)－(32－a2)＝7（cm2）．
故答案为：25－2a2；7．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
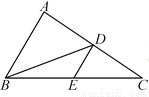
如图，在△ABC中，BD是边AC上的中线，E是BC的中点，连接DE.如果△BDE的面积为2，那么△ABC的面积为______．
8
【解析】∵E是BC的中点,
∴ ,
∵BD是边AC上的中线,
∴ ,
∴,
又△BDE的面积为2，
∴△ABC的面积为8；
故答案是：8. (2x－y)2·(2x＋y)2
16x4－8x2y2＋y4
【解析】试题分析：根据积的乘方的运算法则把(2x－y)2·(2x＋y)2转化为后，先利用平方差公式计算，再利用完全平方公式计算即可.
试题解析：
(2x－y)2·(2x＋y)2
=
=
=16x4－8x2y2＋y4 若□×3xy＝3x2y，则□内应填的单项式是( )
A. xy B. 3xy C. x D. 3x
C
【解析】试题分析：根据题意列出算式，计算即可得到结果．
【解析】
根据题意得：3x2y÷3xy=x，
故选：C 我们规定，若关于x的一元一次方程ax=b的解为b﹣a，则称该方程为“差解方程”，例如：2x=4的解为2，且2=4﹣2，则该方程2x﹣4是差解方程．
（1）判断3x=4.5是否是差解方程；
（2）若关于x的一元一次方程5x=m+1是差解方程，求m的值．
（1）是；（2）m的值为．
【解析】试题分析：（1）求出方程的解，根据差解方程的意义得出即可；
（2）根据差解方程得出关于的方程，求出方程的解即可．
试题解析：
（1）∵ ，
∴，
∵，
∴是差解方程；
（2）∵ 关于的一元一次方程是差解方程，
∴
解得： ，
所以的值为． 某校组织七年级学生参加社会实践活动，若租用45座的客车a辆，则余下的15人无座位；若租用60座的客车则可以少租用1辆，且最后一辆车还有空余的座位，那么乘坐最后一辆60座客车的学生数是（ ）
A. 75-15a B. 135-15a C. 75+15a D. 135-60a
B
【解析】试题分析：总人数为：45a＋15，
则最后一辆车的人数为：45a＋15－60(a－2)＝135－15a．
故选B． 下列方程中，解为x=-3的方程是（ ）
A.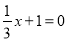 
B. 2x-1=8-x C. -3x=1 D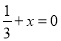
A
【解析】试题分析：A、把x＝－3代入方程x＋1＝0得：左边＝0，右边＝0，
左边＝右边，
所以x＝－3是方程的解，故本选项符合题意；
B、把x＝－3代入方程2x－1＝8－x得：左边＝－7，右边＝11，
左边≠右边，
所以x＝－3不是方程的解，故本选项不符合题意；
C、把x＝－3代入方程－3x＝1得：左边＝9，右边＝1，
左边≠右边，
所以x... 我们已经学过用面积来说明公式，如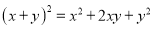
就可以用如图甲中的面积来说明．
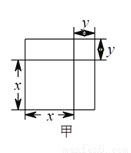
请写出图乙的面积所说明的公式：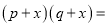 
__________．
【解析】试题解析：∵如图示：大矩形的长、宽分别为(x+p),(x+q),则其面积为：(x+p)?(x+q),从图形关系上可得大矩形为一个边长为x的正方形和三个小矩形构成的则其面积又可表示为： .
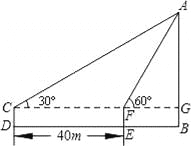
故答案为： . 如图，在一次数学课外实践活动中，要求测教学楼的高度AB、小刚在D处用高1.5m的测角仪CD，测得教学楼顶端A的仰角为30°，然后向教学楼前进40m到达E，又测得教学楼顶端A的仰角为60°．求这幢教学楼的高度AB．
米
【解析】试题分析：首先根据Rt△AFG中∠AFG的正切值得出FG的长度，然后根据∠ACG的正切得出CG的长度，然后根据CG－FG=40得出AG的长度，从而得出AB的长度.
试题解析：在Rt△AFG中，tan∠AFG=∴FG=
在Rt△ACG中， tan∠ACG=∴CG=又CG-FG=40
即AG-=40 ∴AG=20∴AB=20+1.5
答：这幢教学楼的高度AB为...