题目内容
9.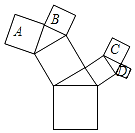 如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为10cm,正方形A的边长为6cm、B的边长为5cm、C的边长为5cm,则正方形D的边长为( )
如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为10cm,正方形A的边长为6cm、B的边长为5cm、C的边长为5cm,则正方形D的边长为( )| A. | $\sqrt{14}$cm | B. | 4 cm | C. | $\sqrt{15}$cm | D. | 3 cm |
分析 先求出SA、SB、SC的值,再根据勾股定理的几何意义求出D的面积,从而求出正方形D的边长.
解答 解:∵SA=6×6=36cm2,
SB=5×5=25cm2,
SC=5×5=25cm2,
又∵SA+SB+SC+SD=10×10,
∴36+25+25+SD=100,
∴SD=14,
∴正方形D的边长为$\sqrt{14}$cm.
故选:A.
点评 本题考查了勾股定理,熟悉勾股定理的几何意义是解题的关键.

练习册系列答案
相关题目
14.$\sqrt{2a}$•$\sqrt{6ab}$等于( )
| A. | a $\sqrt{12ab}$ | B. | 12a2b | C. | a2$\sqrt{12b}$ | D. | 2a $\sqrt{3b}$ |
19.下列给出的x的值,是方程x-6=2x+5的解的是( )
| A. | $x=-\frac{1}{3}$ | B. | x=-1 | C. | x=-11 | D. | $x=\frac{11}{3}$ |
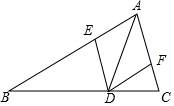 如图,在△ABC中,AD是角平分线,DE∥AC,DF∥AB,求证:四边形AEDF是菱形.
如图,在△ABC中,AD是角平分线,DE∥AC,DF∥AB,求证:四边形AEDF是菱形.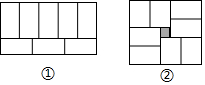 小亮用8个同样大小的长方形,拼成了一个大的长方形(图①).小莹用这8个长方形拼成了正方形(图②),但是中间空出了一个边长为2的小正方形,你能根据图①和图②求出小长方形的长和宽吗?
小亮用8个同样大小的长方形,拼成了一个大的长方形(图①).小莹用这8个长方形拼成了正方形(图②),但是中间空出了一个边长为2的小正方形,你能根据图①和图②求出小长方形的长和宽吗? 如图,已知AB=24cm,CD=10cm,E,F分别为AC,BD的中点,求EF的长.
如图,已知AB=24cm,CD=10cm,E,F分别为AC,BD的中点,求EF的长. 如图,甲、乙两盏路灯相距20米,一天晚上,当小刚从灯甲底部向灯乙底部直行16米时,发现自己的身影顶部正好接触到路灯乙的底部.已知小刚的身高为1.6米,那么路灯甲的高为8米.
如图,甲、乙两盏路灯相距20米,一天晚上,当小刚从灯甲底部向灯乙底部直行16米时,发现自己的身影顶部正好接触到路灯乙的底部.已知小刚的身高为1.6米,那么路灯甲的高为8米.