题目内容
11.解方程组:(1)$\left\{\begin{array}{l}x-2y=0\\ 2x+3y=21\end{array}\right.$
(2)$\left\{\begin{array}{l}5x-2y=4\\ \frac{x}{2}+\frac{y}{3}=2\end{array}\right.$.
分析 (1)方程组利用加减消元法求出解即可;
(2)方程组整理后,利用加减消元法求出解即可.
解答 解:(1)$\left\{\begin{array}{l}{x-2y=0①}\\{2x+3y=21②}\end{array}\right.$,
①×2-②得:-4y=-21,即y=3,
把y=3代入①得:x=6,
则方程组的解为$\left\{\begin{array}{l}{x=6}\\{y=3}\end{array}\right.$;
(2)方程组整理得:$\left\{\begin{array}{l}{5x-2y=4①}\\{3x+2y=12②}\end{array}\right.$,
①+②得:8x=16,即x=2,
把x=2代入①得:y=3,
则方程组的解为$\left\{\begin{array}{l}x=2\\ y=3\end{array}\right.$.
点评 此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.

练习册系列答案
 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案
相关题目
1.化简$\frac{-3\sqrt{3}}{\sqrt{18}}$的结果是( )
| A. | -$\frac{\sqrt{6}}{2}$ | B. | -$\frac{\sqrt{3}}{2}$ | C. | -$\frac{3}{\sqrt{2}}$ | D. | -$\sqrt{3}$ |
2. 直线AB∥CD,∠ABE=30°,∠ECD=100°,则∠BEC=( )
直线AB∥CD,∠ABE=30°,∠ECD=100°,则∠BEC=( )
 直线AB∥CD,∠ABE=30°,∠ECD=100°,则∠BEC=( )
直线AB∥CD,∠ABE=30°,∠ECD=100°,则∠BEC=( )| A. | 120° | B. | 130° | C. | 100° | D. | 110° |
20.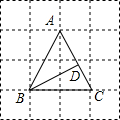 如图所示,△ABC的顶点A、B、C在边长为1的正方形网格的格点上,BD⊥AC于点D,则BD的长为( )
如图所示,△ABC的顶点A、B、C在边长为1的正方形网格的格点上,BD⊥AC于点D,则BD的长为( )
 如图所示,△ABC的顶点A、B、C在边长为1的正方形网格的格点上,BD⊥AC于点D,则BD的长为( )
如图所示,△ABC的顶点A、B、C在边长为1的正方形网格的格点上,BD⊥AC于点D,则BD的长为( )| A. | $\frac{4}{5}\sqrt{5}$ | B. | $\frac{2}{3}\sqrt{5}$ | C. | $\frac{2}{5}\sqrt{5}$ | D. | $\frac{4}{3}\sqrt{3}$ |
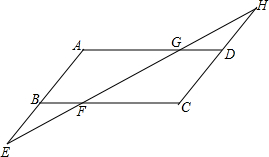 已知,如图,点E、H分别为?ABCD的边AB和CD延长线上一点,且BE=DH,EH分别交BC、AD于点F、G.求证:△AEG≌△CHF.
已知,如图,点E、H分别为?ABCD的边AB和CD延长线上一点,且BE=DH,EH分别交BC、AD于点F、G.求证:△AEG≌△CHF.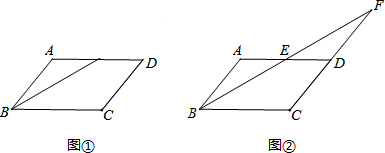
 如图,以平行四边形ABCO的顶点O为原点,边OC所在直线为x轴,建立平面直角坐标系,顶点A、C的坐标分别是(2,4)、(3,0),过点A的反比例函数y=$\frac{k}{x}$(x>0)的图象交BC于D,连接AD,则△ABD的面积是( )
如图,以平行四边形ABCO的顶点O为原点,边OC所在直线为x轴,建立平面直角坐标系,顶点A、C的坐标分别是(2,4)、(3,0),过点A的反比例函数y=$\frac{k}{x}$(x>0)的图象交BC于D,连接AD,则△ABD的面积是( )