题目内容
20.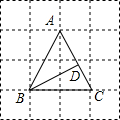 如图所示,△ABC的顶点A、B、C在边长为1的正方形网格的格点上,BD⊥AC于点D,则BD的长为( )
如图所示,△ABC的顶点A、B、C在边长为1的正方形网格的格点上,BD⊥AC于点D,则BD的长为( )| A. | $\frac{4}{5}\sqrt{5}$ | B. | $\frac{2}{3}\sqrt{5}$ | C. | $\frac{2}{5}\sqrt{5}$ | D. | $\frac{4}{3}\sqrt{3}$ |
分析 根据图形和三角形的面积公式求出△ABC的面积,根据勾股定理求出AC,根据三角形的面积公式计算即可.
解答  解:△ABC的面积=$\frac{1}{2}$×BC×AE=2,
解:△ABC的面积=$\frac{1}{2}$×BC×AE=2,
由勾股定理得,AC=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$,
则$\frac{1}{2}$×$\sqrt{5}$×BD=2,
解得BD=$\frac{4}{5}$$\sqrt{5}$,
故选:A.
点评 本题考查的是勾股定理的应用,掌握在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解题的关键.

练习册系列答案
相关题目
10. 小亮同学参加周末社会实践活动,到城郊蔬菜大棚中收集到20株西红柿秧上小西红柿的个数:
小亮同学参加周末社会实践活动,到城郊蔬菜大棚中收集到20株西红柿秧上小西红柿的个数:
32 39 45 55 60 54 60 28 56 41
51 36 44 46 40 53 37 47 45 46
(1)将这20个数按组距为8进行分组,请补全频数分布表及频数分布直方图(如图所示)
(2)观察频数分布直方图,就此大棚中西红柿的长势情况写出一条结论.
 小亮同学参加周末社会实践活动,到城郊蔬菜大棚中收集到20株西红柿秧上小西红柿的个数:
小亮同学参加周末社会实践活动,到城郊蔬菜大棚中收集到20株西红柿秧上小西红柿的个数:32 39 45 55 60 54 60 28 56 41
51 36 44 46 40 53 37 47 45 46
(1)将这20个数按组距为8进行分组,请补全频数分布表及频数分布直方图(如图所示)
| 分组 | 28≤x<36 | 36≤x<44 | 44≤x<52 | 52≤x<60 | 60≤x<68 |
| 频数 | 2 | 2 |
5.如果一个角的两边和另一个角的两边互相平行,那么这两个角之间关系为( )
| A. | 相等 | B. | 互补 | C. | 相等或互补 | D. | 不能确定 |
12.下列计算正确的是( )
| A. | a2•a3=a6 | B. | (a2)3=a5 | C. | (ab)2=a2b2 | D. | (-ab2)2=-a2b4 |
10.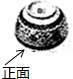 如图,将一只青花碗放在水平桌面上,它的左视图是( )
如图,将一只青花碗放在水平桌面上,它的左视图是( )
 如图,将一只青花碗放在水平桌面上,它的左视图是( )
如图,将一只青花碗放在水平桌面上,它的左视图是( )| A. |  | B. | 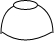 | C. |  | D. | 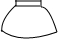 |