Question

16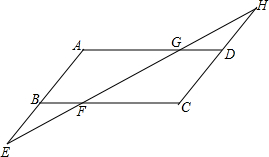．已知，如图，点E、H分别为?ABCD的边AB和CD延长线上一点，且BE=DH，EH分别交BC、AD于点F、G．求证：△AEG≌△CHF．

Answer 1

分析 根据平行四边形的性质可得出AB∥CD，AB=CD，∠A=∠C，再根据平行线的性质得出∠E=∠H，利用ASA即可得出结论．

解答 证明：在?ABCD中，AB∥CD，AB=CD，∠A=∠C，
∴∠E=∠H，
∵BE=DH，
∴AE=CH，
在△AEG与△CHF中，
$\left\{\begin{array}{l}{∠A=∠C}&{\;}\\{AE=CH}&{\;}\\{∠E=∠H}&{\;}\end{array}\right.$，
∴△AEG≌△CHF（ASA）．

点评 本题考查了平行四边形的性质及全等三角形的判定；熟练掌握平行四边形的性质，证明三角形全等是解决问题的关键．