题目内容
1. 如图,以平行四边形ABCO的顶点O为原点,边OC所在直线为x轴,建立平面直角坐标系,顶点A、C的坐标分别是(2,4)、(3,0),过点A的反比例函数y=$\frac{k}{x}$(x>0)的图象交BC于D,连接AD,则△ABD的面积是( )
如图,以平行四边形ABCO的顶点O为原点,边OC所在直线为x轴,建立平面直角坐标系,顶点A、C的坐标分别是(2,4)、(3,0),过点A的反比例函数y=$\frac{k}{x}$(x>0)的图象交BC于D,连接AD,则△ABD的面积是( )| A. | 9 | B. | 6 | C. | 3 | D. | 2 |
分析 先求出反比例函数和直线BC的解析式,再求出由两个解析式组成方程组的解,得出点D的坐标,得出D为BC的中点,△ABD的面积=$\frac{1}{4}$平行四边形ABCD的面积.
解答 解:∵四边形ABCD是平行四边形,A、C的坐标分别是(2,4)、(3,0),
∴点B的坐标为:(5,4),
把点A(2,4)代入反比例函数y=$\frac{k}{x}$得:k=8,
∴反比例函数的解析式为:y=$\frac{8}{x}$;
设直线BC的解析式为:y=kx+b,
把点B(5,4),C(3,0)代入得:$\left\{\begin{array}{l}{5k+b=4}\\{3k+b=0}\end{array}\right.$,
解得:k=2,b=-6,
∴直线BC的解析式为:y=2x-6,
解方程组$\left\{\begin{array}{l}{y=2x-6}\\{y=\frac{8}{x}}\end{array}\right.$ 得:$\left\{\begin{array}{l}{x=4}\\{y=2}\end{array}\right.$,或 $\left\{\begin{array}{l}{x=-1}\\{y=-8}\end{array}\right.$(不合题意,舍去),
∴点D的坐标为:(4,2),
即D为BC的中点,
∴△ABD的面积=$\frac{1}{4}$平行四边形ABCD的面积=$\frac{1}{4}$×(5-2)×4=3.
故选C.
点评 本题考查了平行四边形的性质、用待定系数法求一次函数的解析式、平行四边形和三角形面积的计算;熟练掌握平行四边形的性质,并能进行推理计算是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.下列计算正确的是( )
| A. | a2•a3=a6 | B. | (a2)3=a5 | C. | (ab)2=a2b2 | D. | (-ab2)2=-a2b4 |
10.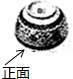 如图,将一只青花碗放在水平桌面上,它的左视图是( )
如图,将一只青花碗放在水平桌面上,它的左视图是( )
 如图,将一只青花碗放在水平桌面上,它的左视图是( )
如图,将一只青花碗放在水平桌面上,它的左视图是( )| A. |  | B. | 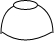 | C. |  | D. | 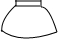 |
 如图,两个全等的直角三角形重叠在一起,将其中的一个三角形沿着点B到C的方向平移到△DEF的位置,AB=10,DO=4,平移距离为6,则阴影部分面积为( )
如图,两个全等的直角三角形重叠在一起,将其中的一个三角形沿着点B到C的方向平移到△DEF的位置,AB=10,DO=4,平移距离为6,则阴影部分面积为( )