题目内容
13.下列图形中,(1)角;(2)等边三角形;(3)平行四边形.若是轴对称图形,画出它所有的对称轴;若是中心对称图形,找出它的对称中心(用点O表示).
分析 根据轴对称图形和中心对称图形的定义即可判断.
解答 解:如图所示:
点评 本题主要考查轴对称图形和中心对称图形,掌握等边三角形和平行四边形的性质及角平分线的定义是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
4.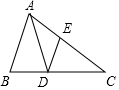 如图,已知AD为△ABC的角平分线,DE∥AB交AC于E,如果$\frac{AE}{EC}$=$\frac{3}{5}$,那么$\frac{AC}{AB}$等于( )
如图,已知AD为△ABC的角平分线,DE∥AB交AC于E,如果$\frac{AE}{EC}$=$\frac{3}{5}$,那么$\frac{AC}{AB}$等于( )
 如图,已知AD为△ABC的角平分线,DE∥AB交AC于E,如果$\frac{AE}{EC}$=$\frac{3}{5}$,那么$\frac{AC}{AB}$等于( )
如图,已知AD为△ABC的角平分线,DE∥AB交AC于E,如果$\frac{AE}{EC}$=$\frac{3}{5}$,那么$\frac{AC}{AB}$等于( )| A. | $\frac{3}{5}$ | B. | $\frac{5}{3}$ | C. | $\frac{8}{5}$ | D. | $\frac{3}{2}$ |
8.函数y=$\frac{\sqrt{x-2}}{x+4}$中,自变量x的取值范围是( )
| A. | x>4 | B. | x≥2 | C. | x≥2且x≠-4 | D. | x≠-4 |
18.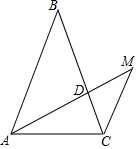 如图,若AB=BC,∠BAC=70°,AD=BD,CM∥AB交AD的延长线于点M,则∠M的大小是( )
如图,若AB=BC,∠BAC=70°,AD=BD,CM∥AB交AD的延长线于点M,则∠M的大小是( )
 如图,若AB=BC,∠BAC=70°,AD=BD,CM∥AB交AD的延长线于点M,则∠M的大小是( )
如图,若AB=BC,∠BAC=70°,AD=BD,CM∥AB交AD的延长线于点M,则∠M的大小是( )| A. | 60° | B. | 70° | C. | 30° | D. | 40° |
2.果农计划对果园加大种植密度,据测算,果园的总产量y(个)与增种果树的棵数x(棵)间的函数关系式为y=
-5x2+100x+60000,要使总产量在60320个以上,需要增加果树的棵数范围是( )
-5x2+100x+60000,要使总产量在60320个以上,需要增加果树的棵数范围是( )
| A. | 4≤x≤16 | B. | x≥6或x≤16 | C. | 4<x<16 | D. | x>6或x<16 |
3.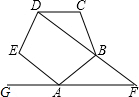 如图,正五边形ABCDE,AF∥CD,交DB的延长线于点F,则∠DFA=( )
如图,正五边形ABCDE,AF∥CD,交DB的延长线于点F,则∠DFA=( )
 如图,正五边形ABCDE,AF∥CD,交DB的延长线于点F,则∠DFA=( )
如图,正五边形ABCDE,AF∥CD,交DB的延长线于点F,则∠DFA=( )| A. | 108° | B. | 72° | C. | 36° | D. | 30° |
 如图,△ABC中,DE∥BC,则$\frac{AB}{()}$=$\frac{()}{()}$.
如图,△ABC中,DE∥BC,则$\frac{AB}{()}$=$\frac{()}{()}$.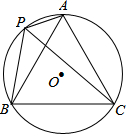 如图,⊙O的半径为1,A、P、B、C是⊙O上的四个点.∠APC=∠CPB=60°.则四边形APBC的最大面积是√3.
如图,⊙O的半径为1,A、P、B、C是⊙O上的四个点.∠APC=∠CPB=60°.则四边形APBC的最大面积是√3.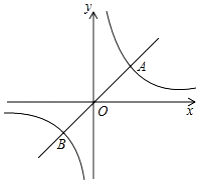 如图,定义:若双曲线y=$\frac{k}{x}$(k>0)与它的其中一条对称轴y=x相交于A、B两点,则线段AB的长度为双曲线y=$\frac{k}{x}$(k>0)的对径.
如图,定义:若双曲线y=$\frac{k}{x}$(k>0)与它的其中一条对称轴y=x相交于A、B两点,则线段AB的长度为双曲线y=$\frac{k}{x}$(k>0)的对径.