题目内容
1.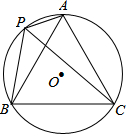 如图,⊙O的半径为1,A、P、B、C是⊙O上的四个点.∠APC=∠CPB=60°.则四边形APBC的最大面积是√3.
如图,⊙O的半径为1,A、P、B、C是⊙O上的四个点.∠APC=∠CPB=60°.则四边形APBC的最大面积是√3.
分析 过C作直径CP′,连接P′A、P′B,如图,先利用圆周角定理得到∠ABC=∠APC=60°,∠BAC=∠CPB=60°,则可判断△ABC为等边三角形,再利用圆周角定理得到∠CAP′=∠CBP′=90°,利用含30度的直角三角形三边的关系得到P′A=P′B=$\frac{1}{2}$CP′=1,AC=BC=$\sqrt{3}$,所以四边形AP′BC的面积为$\sqrt{3}$,由于点P运动到点P′的位置时,四边形APBC的最大面积,从而得到四边形APBC的最大面积.
解答 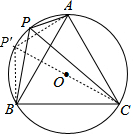 解:过C作直径CP′,连接P′A、P′B,如图,
解:过C作直径CP′,连接P′A、P′B,如图,
∵∠ABC=∠APC=60°,∠BAC=∠CPB=60°,
∴△ABC为等边三角形,
∵CP′为直径,
∴∠CAP′=∠CBP′=90°,
而∠AP′C=∠APC=60°,∠BP′C=∠BPC=60°,
∴P′A=P′B=$\frac{1}{2}$CP′=1,AC=BC=$\sqrt{3}$,
∴四边形AP′BC的面积为2×$\frac{1}{2}$×1×$\sqrt{3}$=$\sqrt{3}$,
当点P运动到点P′的位置时,四边形APBC的最大面积,即四边形APBC的最大面积为$\sqrt{3}$.
故答案为$\sqrt{3}$.
点评 本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.推论:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
7.下列计算中,错误的是( )
| A. | -x2•x3=-x5 | B. | (x-1)2=x2-1 | C. | x6÷(-x3)=-x3 | D. | x2-2x2=-x2 |
9.备受关注的象山港跨海大桥总投资约77亿元,77亿元用科学记数法表示为( )
| A. | 7.7×109元 | B. | 7.7×1010元 | C. | 0.77×1010元 | D. | 0.77×1011元 |
11.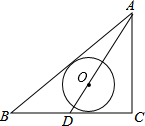 如图,△ABC中,∠C=90°,AC=3,AB=5,D为BC边的中点,以AD上一点O为圆心的⊙O和AB、BC均相切,则⊙O的半径为( )
如图,△ABC中,∠C=90°,AC=3,AB=5,D为BC边的中点,以AD上一点O为圆心的⊙O和AB、BC均相切,则⊙O的半径为( )
 如图,△ABC中,∠C=90°,AC=3,AB=5,D为BC边的中点,以AD上一点O为圆心的⊙O和AB、BC均相切,则⊙O的半径为( )
如图,△ABC中,∠C=90°,AC=3,AB=5,D为BC边的中点,以AD上一点O为圆心的⊙O和AB、BC均相切,则⊙O的半径为( )| A. | 1 | B. | $\frac{6}{7}$ | C. | $\frac{2}{3}$ | D. | 1.5 |

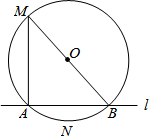 已知⊙O的半径是2,直线l与⊙O相交于A、B两点.M是⊙O上的一个动点,若∠AMB=45°,则△AMB面积的最大值是2$\sqrt{2}$+2.
已知⊙O的半径是2,直线l与⊙O相交于A、B两点.M是⊙O上的一个动点,若∠AMB=45°,则△AMB面积的最大值是2$\sqrt{2}$+2.