题目内容
18.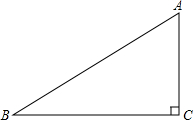 如图,在Rt△ABC中,∠C=90°
如图,在Rt△ABC中,∠C=90°(1)用直尺和圆规作图:
①作∠A的平分线交BC于D;
②作⊙O,使得圆心O在AB上且圆经过点A、D.
(2)判定⊙O与BC的位置关系,并证明你结论;
(3)若所作的圆与AB交于点E,AC=3,AE=4,求AD的值.
分析 (1)作出∠BAC的角平分线即可得到点D,再作出AD的垂直平分线与AB交于点O,以OA长为半径就可以作出符合要求的圆;
(2)利用角平分线性质证得OD∥AC就可以证出BC与⊙O相切;
(3)连接DE,证明△AED∽△ADC,利用边对应成比例可以求出AD的长.
解答 解:(1)如图所示:
作∠BAC角平分线AD,与BC交于点D,则点D为所求;
作AD垂直平分线,与AB交于点O,以OA长为半径画圆,则⊙O为所求.
(2)⊙O与BC相切
连接OD,如图2所示:
∵OA=OD,
∴∠OAD=∠ODA,
∵AD平分∠BAC,
∴∠OAD=∠DAC,
∴∠ODA=∠DAC,
∴OD∥AC,
∵∠C=90°,
∴∠ODB=∠C=90°,
∴⊙O与BC相切
(3)连接DE,如图3所示:
∵AE为直径,
∴∠ADE=90°,
∵∠EAD=∠DAC,∠C=90°,
∴△AED∽△ADC
∴$\frac{AE}{AD}=\frac{AD}{AC}$,
∵AC=3,AE=4,
∴AD2=3×4=12,则AD=2$\sqrt{3}$.
点评 本题考查了角平分线及垂直平分线的作法,还考查了切线性质、相似三角形性质.根据题意作出辅助线,构造出相似三角形是解答此题的关键.

练习册系列答案
相关题目
6.下列命题中,真命题是( )
| A. | 有两边相等的平行四边形是菱形 | |
| B. | 有一个角是直角的四边形是矩形 | |
| C. | 四个角相等的菱形是正方形 | |
| D. | 两条对角线互相垂直且相等的四边形是正方形 |
3.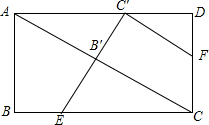 如图,在矩形ABCD中,点E在BC上,将△ABE沿AE翻折,点B恰好落在对角线AC上的B′处,点F在CD上,将△ECF沿EF翻折,点C恰好落在AD上的C′处,若E、B′C′三点共线,则$\frac{CF}{AB}$=( )
如图,在矩形ABCD中,点E在BC上,将△ABE沿AE翻折,点B恰好落在对角线AC上的B′处,点F在CD上,将△ECF沿EF翻折,点C恰好落在AD上的C′处,若E、B′C′三点共线,则$\frac{CF}{AB}$=( )
 如图,在矩形ABCD中,点E在BC上,将△ABE沿AE翻折,点B恰好落在对角线AC上的B′处,点F在CD上,将△ECF沿EF翻折,点C恰好落在AD上的C′处,若E、B′C′三点共线,则$\frac{CF}{AB}$=( )
如图,在矩形ABCD中,点E在BC上,将△ABE沿AE翻折,点B恰好落在对角线AC上的B′处,点F在CD上,将△ECF沿EF翻折,点C恰好落在AD上的C′处,若E、B′C′三点共线,则$\frac{CF}{AB}$=( )| A. | $\frac{\sqrt{2}}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{3}{4}$ |
10.若不等式组$\left\{\begin{array}{l}{x<2a-1}\\{x>3}\end{array}\right.$无解,则a的取值范围是( )
| A. | a≤2 | B. | a>2 | C. | a>3 | D. | a≥3 |
8.一元二次方程(x+1)2-2(x-1)2=7的根的情况是( )
| A. | 无实数根 | B. | 有一正根一负根 | C. | 有两个正根 | D. | 有两个负根 |
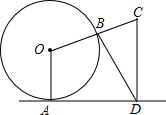 如图,直线l与⊙O相切于点A,作半径OB并延长至点C,使得BC=OB,作CD⊥直线l于点D,连接BD得∠CBD=75°,则∠OCD=70度.
如图,直线l与⊙O相切于点A,作半径OB并延长至点C,使得BC=OB,作CD⊥直线l于点D,连接BD得∠CBD=75°,则∠OCD=70度. 如图,正方形AOCB在平面直角坐标系x0y中,点O为原点,点B在反比例函数y=$\frac{16}{x}$(x>0)图象上.
如图,正方形AOCB在平面直角坐标系x0y中,点O为原点,点B在反比例函数y=$\frac{16}{x}$(x>0)图象上.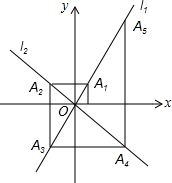 如图,在平面直角坐标系中,函数y=2x和y=-x的图象分别为直线l1,l2,过点(1,0)作x轴的垂线交l1于点A1,过点A1作y轴的垂线交l2于点A2,过点A2作x轴的垂线交l1于点A3,过点A3作y轴的垂线交l2于点A4,…依次进行下去,则点A2017的坐标为(21008,21009).
如图,在平面直角坐标系中,函数y=2x和y=-x的图象分别为直线l1,l2,过点(1,0)作x轴的垂线交l1于点A1,过点A1作y轴的垂线交l2于点A2,过点A2作x轴的垂线交l1于点A3,过点A3作y轴的垂线交l2于点A4,…依次进行下去,则点A2017的坐标为(21008,21009).