题目内容
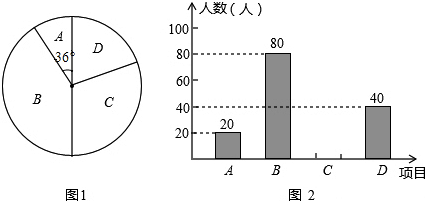
7. 如图,在平面直角坐标系中,函数y=2x和y=-x的图象分别为直线l1,l2,过点(1,0)作x轴的垂线交l1于点A1,过点A1作y轴的垂线交l2于点A2,过点A2作x轴的垂线交l1于点A3,过点A3作y轴的垂线交l2于点A4,…依次进行下去,则点A2017的坐标为(21008,21009).
如图,在平面直角坐标系中,函数y=2x和y=-x的图象分别为直线l1,l2,过点(1,0)作x轴的垂线交l1于点A1,过点A1作y轴的垂线交l2于点A2,过点A2作x轴的垂线交l1于点A3,过点A3作y轴的垂线交l2于点A4,…依次进行下去,则点A2017的坐标为(21008,21009).
分析 写出部分An点的坐标,根据坐标的变化找出变化规律“A2n+1((-2)n,2(-2)n)(n为自然数)”,依此规律即可得出结论.
解答 解:观察,发现规律:A1(1,2),A2(-2,2),A3(-2,-4),A4(4,-4),A5(4,8),…,
∴A2n+1((-2)n,2(-2)n)(n为自然数).
∵2017=1008×2+1,
∴A2017的坐标为((-2)1008,2(-2)1008)=(21008,21009).
故答案为:(21008,21009).
点评 本题考查了一次函数图象上点的坐标特征以及规律型中坐标的变化,解题的关键是找出变化规律“A2n+1((-2)n,2(-2)n)(n为自然数)”.本题属于基础题,难度不大,解决该题型题目时,写出部分An点的坐标,根据坐标的变化找出变化规律是关键.

练习册系列答案
相关题目
17.若关于x的方程$\frac{2x-a}{x-1}$=1无解,则a的值为( )
| A. | 0 | B. | 1 | C. | 2 | D. | 4 |
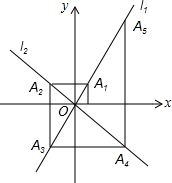
15. 如图所示,在菱形ABCD中,BC=2,∠B=60°,E为BC的中点,点F在AB边上,连接EF,将△BEF沿EF翻折,使点B落在点B′处,连接AB′,则AB′的最小值是( )
如图所示,在菱形ABCD中,BC=2,∠B=60°,E为BC的中点,点F在AB边上,连接EF,将△BEF沿EF翻折,使点B落在点B′处,连接AB′,则AB′的最小值是( )
 如图所示,在菱形ABCD中,BC=2,∠B=60°,E为BC的中点,点F在AB边上,连接EF,将△BEF沿EF翻折,使点B落在点B′处,连接AB′,则AB′的最小值是( )
如图所示,在菱形ABCD中,BC=2,∠B=60°,E为BC的中点,点F在AB边上,连接EF,将△BEF沿EF翻折,使点B落在点B′处,连接AB′,则AB′的最小值是( )| A. | 2-$\sqrt{3}$ | B. | $\sqrt{3}$+1 | C. | 2+$\sqrt{3}$ | D. | $\sqrt{3}$-1 |
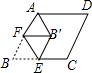
17. 自来水公司调查了若干用户的月用水量x(单位:吨),按月用水量将用户分成A、B、C、D、E五组进行统计,并制作了如图所示的扇形统计图.已知除B组以外,参与调查的用户共64户,则所有参与调查的用户中月用水量在6吨以下的共有( )
自来水公司调查了若干用户的月用水量x(单位:吨),按月用水量将用户分成A、B、C、D、E五组进行统计,并制作了如图所示的扇形统计图.已知除B组以外,参与调查的用户共64户,则所有参与调查的用户中月用水量在6吨以下的共有( )
 自来水公司调查了若干用户的月用水量x(单位:吨),按月用水量将用户分成A、B、C、D、E五组进行统计,并制作了如图所示的扇形统计图.已知除B组以外,参与调查的用户共64户,则所有参与调查的用户中月用水量在6吨以下的共有( )
自来水公司调查了若干用户的月用水量x(单位:吨),按月用水量将用户分成A、B、C、D、E五组进行统计,并制作了如图所示的扇形统计图.已知除B组以外,参与调查的用户共64户,则所有参与调查的用户中月用水量在6吨以下的共有( ) | 组别 | 月用水量x(单位:吨) |
| A | 0≤x<3 |
| B | 3≤x<6 |
| C | 6≤x<9 |
| D | 9≤x<12 |
| E | x≥12 |
| A. | 18户 | B. | 20户 | C. | 22户 | D. | 24户 |
 如图,在Rt△ABC中,∠C=90°
如图,在Rt△ABC中,∠C=90°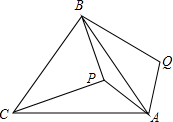 如图,P是等边三角形ABC内一点,将线段AP绕点A顺时针旋转60°得到线段AQ,连接BQ.若PA=6,PB=8,PC=10,则四边形APBQ的面积为24+9$\sqrt{3}$.
如图,P是等边三角形ABC内一点,将线段AP绕点A顺时针旋转60°得到线段AQ,连接BQ.若PA=6,PB=8,PC=10,则四边形APBQ的面积为24+9$\sqrt{3}$.