题目内容
9.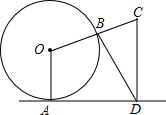 如图,直线l与⊙O相切于点A,作半径OB并延长至点C,使得BC=OB,作CD⊥直线l于点D,连接BD得∠CBD=75°,则∠OCD=70度.
如图,直线l与⊙O相切于点A,作半径OB并延长至点C,使得BC=OB,作CD⊥直线l于点D,连接BD得∠CBD=75°,则∠OCD=70度.
分析 过点B作BE⊥AD于点D,连接AB,利用BC=OB、CD⊥AD及AD为⊙O切线可证得△BAD为等腰三角形,此时可利用∠BAD=∠BDA找到∠C与∠O的关系,从而可以求出∠C的度数.
解答 解:过点B作BE⊥AD于点D,连接AB,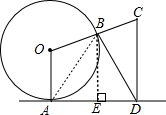
∵直线l与⊙O相切于点A,
∴OA⊥AD,
∵CD⊥AD,
∴OA∥BE∥CD,
∴∠O+∠C=180°,
∵OB=BC,
∴AE=ED,
∴BA=BD,
∴∠BAE=∠BDE,
∵直线l与⊙O相切于点A,
∴∠O=2∠BAE,
∴∠O=2∠BDE,
∵∠CBD=75°,CD⊥AD,
∴∠BDC=105°-∠C,∠BDE=90°-(105°-∠C)=∠C-15°,
∴∠O=2(∠C-15°)=2∠C-30°,
∴2∠C-30°+∠C=180°,解得∠C=70°.
故答案为:70.
点评 本题考查了切线的性质、中位线性质、等腰三角形性质,解题的关键是通过辅助线构造等腰三角形,将所求角之间的关系建立起来.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
20.已知a+$\frac{1}{a}$=$\sqrt{7}$,则a-$\frac{1}{a}$的值为( )
| A. | 7 | B. | 4 | C. | ±$\sqrt{3}$ | D. | ±3 |
17.若关于x的方程$\frac{2x-a}{x-1}$=1无解,则a的值为( )
| A. | 0 | B. | 1 | C. | 2 | D. | 4 |
4. 如图是一个正方体的表面展开图,则原正方体标有数字“1”所在面的对面标有数字( )
如图是一个正方体的表面展开图,则原正方体标有数字“1”所在面的对面标有数字( )
 如图是一个正方体的表面展开图,则原正方体标有数字“1”所在面的对面标有数字( )
如图是一个正方体的表面展开图,则原正方体标有数字“1”所在面的对面标有数字( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
 如图,在四边形ABCD中,AD∥BC,AD=8,BC=16,点P以每秒1个单位长度的速度从点A出发,沿AD向点D运动;点Q同时以每秒2个单位长度的速度从点C出发,沿CB向点B运动,点P停止运动时,点Q也随之停止运动,设运动时间为t秒.
如图,在四边形ABCD中,AD∥BC,AD=8,BC=16,点P以每秒1个单位长度的速度从点A出发,沿AD向点D运动;点Q同时以每秒2个单位长度的速度从点C出发,沿CB向点B运动,点P停止运动时,点Q也随之停止运动,设运动时间为t秒.

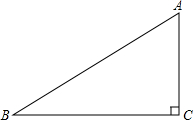 如图,在Rt△ABC中,∠C=90°
如图,在Rt△ABC中,∠C=90°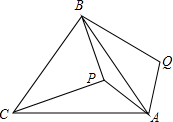 如图,P是等边三角形ABC内一点,将线段AP绕点A顺时针旋转60°得到线段AQ,连接BQ.若PA=6,PB=8,PC=10,则四边形APBQ的面积为24+9$\sqrt{3}$.
如图,P是等边三角形ABC内一点,将线段AP绕点A顺时针旋转60°得到线段AQ,连接BQ.若PA=6,PB=8,PC=10,则四边形APBQ的面积为24+9$\sqrt{3}$.