题目内容
20.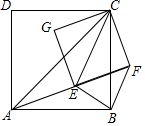 如图,已知AC、EC分别为四边形ABCD和EFCG的对角线,点E在△ABC内,∠CAE+∠CBE=90°,当四边形ABCD和EFCG均为正方形时,连接BF.
如图,已知AC、EC分别为四边形ABCD和EFCG的对角线,点E在△ABC内,∠CAE+∠CBE=90°,当四边形ABCD和EFCG均为正方形时,连接BF.(1)求证:△CAE∽△CBF;
(2)若BE=1,AE=2,求CE的长.
分析 (1)首先根据四边形ABCD和EFCG均为正方形,可得$\frac{AC}{BC}$=$\frac{EC}{FC}$=$\sqrt{2}$,∠ACE=∠BCF;然后根据相似三角形判定的方法,推得△CAE∽△CBF即可;
(2)首先根据△CAE∽△CBF,判断出∠CAE=∠△CBF,再根据∠CAE+∠CBE=90°,判断出∠EBF=90°;然后在Rt△BEF中,根据勾股定理,求出EF的长度,再根据CE、EF的关系,求出CE的长是多少即可.
解答 解:(1)∵四边形ABCD和EFCG均为正方形,
∴$\frac{AC}{BC}$=$\frac{EC}{FC}$=$\sqrt{2}$,
又∵∠ACE+∠BCE=∠BCF+∠BCE=45°,
∴∠ACE=∠BCF,
∴△CAE∽△CBF.
(2):∵△CAE∽△CBF,
∴∠CAE=∠CBF,$\frac{AE}{BF}$=$\frac{AC}{BC}$,
又∵∠CAE+∠CBE=90°,
∴∠CBF+∠CBE=90°,
∴∠EBF=90°,
又∵$\frac{AE}{BF}$=$\frac{AC}{BC}$=$\sqrt{2}$,AE=2
∴$\frac{2}{BF}$=$\sqrt{2}$,
∴BF=$\sqrt{2}$,
∴EF2=BE2+BF2=3,
∴EF=$\sqrt{3}$,
∵CE2=2EF2=6,
∴CE=$\sqrt{6}$.
点评 此题考查相似三角形的判定和性质,正方形的性质,掌握相似三角形的判定方法是解决问题的前提.

练习册系列答案
相关题目
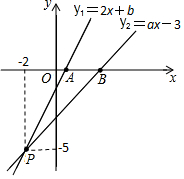 如图,已知函数y1=2x+b和y2=ax-3的图象交于点P (-2,-5),这两个函数的图象与x轴分别交于点A、B.
如图,已知函数y1=2x+b和y2=ax-3的图象交于点P (-2,-5),这两个函数的图象与x轴分别交于点A、B.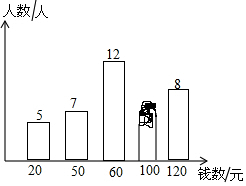 小明调查了学校50名同学本学期购买课外书的花费情况,并将结果绘制成了下面的统计图,由于不小心滴上了墨水,导致花费为100元的人数看不清楚了.求出这50名学生本学期购买课外书花费的众数、中位数和平均数.
小明调查了学校50名同学本学期购买课外书的花费情况,并将结果绘制成了下面的统计图,由于不小心滴上了墨水,导致花费为100元的人数看不清楚了.求出这50名学生本学期购买课外书花费的众数、中位数和平均数.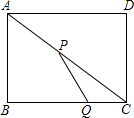 如图,在矩形ABCD中,AB=6,BC=8,动点P以2个单位/秒的速度从点A出发,沿AC向点C移动,同时动点Q以1个单位/秒的速度从点C出发,沿CB向点B移动,当P、Q两点中其中一点到达终点时停止运动,在P、Q两点移动过程中,当△PQC为等腰三角形时,求时间t的值.
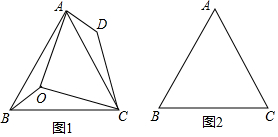
如图,在矩形ABCD中,AB=6,BC=8,动点P以2个单位/秒的速度从点A出发,沿AC向点C移动,同时动点Q以1个单位/秒的速度从点C出发,沿CB向点B移动,当P、Q两点中其中一点到达终点时停止运动,在P、Q两点移动过程中,当△PQC为等腰三角形时,求时间t的值.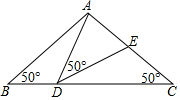 如图,在△ABC中,AB=AC=2,∠B=∠C=50°,点D在线段BC上运动(点D不与B、C重合),连接AD,作∠ADE=50°,DE交线段AC于E.
如图,在△ABC中,AB=AC=2,∠B=∠C=50°,点D在线段BC上运动(点D不与B、C重合),连接AD,作∠ADE=50°,DE交线段AC于E.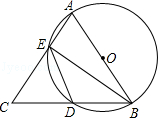 如图,△ABC中,AB=AC,以AB为直径的⊙O交AC,BC分别于点E,D两点,连结ED,BE.
如图,△ABC中,AB=AC,以AB为直径的⊙O交AC,BC分别于点E,D两点,连结ED,BE.