Question

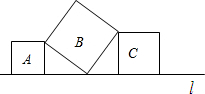如图，直线l上有三个正方形，A，B，C，若A，C的面积分别为36和64，则B的面积为

 

．

Answer 1

考点：全等三角形的判定与性质,勾股定理,正方形的性质

专题：计算题

分析：如图，根据正方形的性质得EF²=36，MN²=64，GE=GM，∠EGM=90°，再利用等角的余角相等可证明∠FEG=∠NGM，则根据“AAS”可判断△EFG≌△GNM，得到GF=MN，然后在Rt△EFG中利用勾股定理得到EG²=EF²+FG²=EG²+MN²=100，所以正方形B的面积为100．

解答：解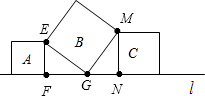：如图，
∵图形A、B、C都是为正方形，
∴EF²=36，MN²=64，GE=GM，∠EGM=90°，
∴∠EGF+∠NGM=90°，
而∠EGF+∠FEG=90°，
∴∠FEG=∠NGM，
在△EFG和△GNM中，

∠EFG=∠NGM ∠FEG=∠NGM EG=GM

，
∴△EFG≌△GNM，
∴GF=MN，
在Rt△EFG中，EG²=EF²+FG²=EG²+MN²=36+64=100，
∴正方形B的面积为100．
故答案为100．

点评：本题考查了全等三角形的判定与性质：全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具．在判定三角形全等时，关键是选择恰当的判定条件．也考查了正方形的性质和勾股定理．