题目内容
 如图,AC、BC是⊙O的两条弦,其中BC>AC,半径OD⊥AB,DE⊥BC于E,
如图,AC、BC是⊙O的两条弦,其中BC>AC,半径OD⊥AB,DE⊥BC于E,求证:AC+CE=BE.
考点:全等三角形的判定与性质,圆心角、弧、弦的关系,圆周角定理
专题:证明题
分析:利用圆周角定理以及垂径定理得出∠DAB=∠DBA,进而得出△DFC≌△DEC(AAS),进而得出Rt△DFA≌Rt△DEB(SAS),进而得出答案.
解答: 证明:连接AD,DB,CD,过点D作DF⊥AC于F,
证明:连接AD,DB,CD,过点D作DF⊥AC于F,
∵OD⊥AB,∴DA=DB,
=
,
∴∠DAB=∠DBA,
∵∠FCD=∠DBA,∠DCB=∠DAB,
∴∠FCD=∠DCB,
而DF⊥AC,DE⊥BC,
∴∠F=∠CED,
在△DFC和△DEC中,
,
∴△DFC≌△DEC(AAS),
∴FC=EC,DF=DE,
在Rt△DFA和Rt△DEB中,
,
∴Rt△DFA≌Rt△DEB(SAS),
∴BE=AF=CA+CF=CA+AE.
 证明:连接AD,DB,CD,过点D作DF⊥AC于F,
证明:连接AD,DB,CD,过点D作DF⊥AC于F,∵OD⊥AB,∴DA=DB,
 |
| DA |
 |
| DE |
∴∠DAB=∠DBA,
∵∠FCD=∠DBA,∠DCB=∠DAB,
∴∠FCD=∠DCB,
而DF⊥AC,DE⊥BC,
∴∠F=∠CED,
在△DFC和△DEC中,
|
∴△DFC≌△DEC(AAS),
∴FC=EC,DF=DE,
在Rt△DFA和Rt△DEB中,
|
∴Rt△DFA≌Rt△DEB(SAS),
∴BE=AF=CA+CF=CA+AE.
点评:此题主要考查了全等三角形的判定与性质以及圆周角定理等知识,得出FC=EC,DF=DE,进而求出Rt△DFA≌Rt△DEB是解题关键.

练习册系列答案
相关题目
下列事件中,必然事件是( )
| A、抛掷1个均匀的骰子,出现6点向上 |
| B、两直线被第三条直线所截,同位角相等 |
| C、366人中至少有2人的生日相同 |
| D、实数的绝对值是非负数 |
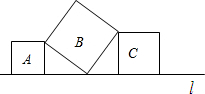 如图,直线l上有三个正方形,A,B,C,若A,C的面积分别为36和64,则B的面积为
如图,直线l上有三个正方形,A,B,C,若A,C的面积分别为36和64,则B的面积为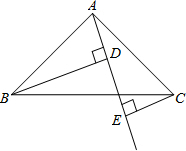 如图,已知△ABC中,∠BAC=90°,AB=AC,AE是过点A的一条直线,且B点和C点在AE的两侧,BD⊥AE于点D,CE⊥AE于点E.
如图,已知△ABC中,∠BAC=90°,AB=AC,AE是过点A的一条直线,且B点和C点在AE的两侧,BD⊥AE于点D,CE⊥AE于点E.
 如图,Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=4cm,D为BC的中点,若动点E以1cm/s的速度从A点出发,沿着A→B→A的方向运动,设E点的运动时间为t秒(0≤t<12),连接DE,当△BDE是直角三角形时,t的值为
如图,Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=4cm,D为BC的中点,若动点E以1cm/s的速度从A点出发,沿着A→B→A的方向运动,设E点的运动时间为t秒(0≤t<12),连接DE,当△BDE是直角三角形时,t的值为