题目内容
 如图,AB=AC,BD=CE,DF⊥CB于F,若BC=a,则GF=( )
如图,AB=AC,BD=CE,DF⊥CB于F,若BC=a,则GF=( )A、
| ||
B、
| ||
C、
| ||
D、
|
考点:全等三角形的判定与性质,等腰三角形的判定与性质
专题:
分析:作EH⊥BC的延长线与H点,证得Rt△BDF≌Rt△CEH后即可证得BF=CH,从而得到BC=FH=a,从而求得FG=
FH=
a.
| 1 |
| 2 |
| 1 |
| 2 |
解答: 解:作EH⊥BC的延长线与H点,
解:作EH⊥BC的延长线与H点,
∵AB=AC,
∴∠B=∠ACB=∠HCE,
在Rt△BDF和Rt△CEH中,
,
∴Rt△BDF≌Rt△CEH(AAS),
∴BF=CH,
∴BC=FH=a,
∴FG=
FH=
a.
故选A.
 解:作EH⊥BC的延长线与H点,
解:作EH⊥BC的延长线与H点,∵AB=AC,
∴∠B=∠ACB=∠HCE,
在Rt△BDF和Rt△CEH中,
|
∴Rt△BDF≌Rt△CEH(AAS),
∴BF=CH,
∴BC=FH=a,
∴FG=
| 1 |
| 2 |
| 1 |
| 2 |
故选A.
点评:本题考查了全等三角形的判定与性质及等腰三角形的判定与性质,属于基础题,能够正确的构造全等三角形是解答本题的关键.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
下列事件中,必然事件是( )
| A、抛掷1个均匀的骰子,出现6点向上 |
| B、两直线被第三条直线所截,同位角相等 |
| C、366人中至少有2人的生日相同 |
| D、实数的绝对值是非负数 |

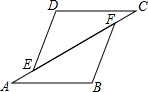 已知:如图,点E、F在线段AC上,AB∥CD,AE=CF,
已知:如图,点E、F在线段AC上,AB∥CD,AE=CF,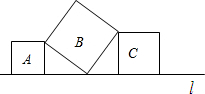 如图,直线l上有三个正方形,A,B,C,若A,C的面积分别为36和64,则B的面积为
如图,直线l上有三个正方形,A,B,C,若A,C的面积分别为36和64,则B的面积为