题目内容
11. 在△ABC,AB=AC,∠BAC=120°,点D在BC上,AD=DE,∠ADE=120°,求∠BCE.
在△ABC,AB=AC,∠BAC=120°,点D在BC上,AD=DE,∠ADE=120°,求∠BCE.
分析 作∠FDC=120°,交CA的延长线与点F,通过SAS可证△DCE≌△DAF,根据全等三角形的性质可得∠BCE=∠DFA=30.
解答  解:如图,作∠FDC=120°,交CA的延长线与点F.
解:如图,作∠FDC=120°,交CA的延长线与点F.
∵∠ADE=∠BAC=120°,
∴∠FDA+∠ADC=∠CDE+∠ADC,∠ACB=30°,
∴∠FDA=∠CDE,∠DFC=∠ACB=30°,DF=DC,
在△FDA与△CDE中,
$\left\{\begin{array}{l}{DF=DC}\\{∠FDA=∠CDE}\\{AD=DE}\end{array}\right.$,
∴△FDA≌△CDE(SAS),
∴∠DCE=∠DFA=30°,
∴∠BCE=30°.
点评 本题主要考查了全等三角形的判定和性质,作辅助线,将问题转化为两个全等的三角形中解答,是解答本题的关键,注意挖掘本题中的隐含条件,以及知识点的熟练应用.

练习册系列答案
相关题目
19.某家庭搬进新居后又添置了新的电冰箱、电热水器等家用电器,为了了解每月用电量的多少,该家庭在6月初连续几天观察电表的千瓦时数,电表显示如表所示:
(1)估计这个家庭六月份的总用电量是多少千瓦时?
(2)用这样的方法估计全年的用电量合适吗?为什么?
(3)你有更合理的方法帮助该家庭估计全年的用电量吗?
| 日期 | 1日 | 2日 | 3日 | 4日 | 5日 | 6日 | 7日 | 8日 |
| 电表显示度数 (度) | 115 | 118 | 122 | 127 | 133 | 136 | 140 | 143 |
(2)用这样的方法估计全年的用电量合适吗?为什么?
(3)你有更合理的方法帮助该家庭估计全年的用电量吗?
3.下列运算正确的是( )
| A. | a2×a3=a6 | B. | 2$\sqrt{3}×\sqrt{3}÷\sqrt{3}=2\sqrt{3}$ | C. | x2-5x+6=(x-6)(x+1) | D. | a2+a3=a5 |
20. 如图,在?ABCD中,E是AD边上的中点,连接BE,并延长BE交CD延长线于点F,则S△EDF与S△BCF的比值是( )
如图,在?ABCD中,E是AD边上的中点,连接BE,并延长BE交CD延长线于点F,则S△EDF与S△BCF的比值是( )
 如图,在?ABCD中,E是AD边上的中点,连接BE,并延长BE交CD延长线于点F,则S△EDF与S△BCF的比值是( )
如图,在?ABCD中,E是AD边上的中点,连接BE,并延长BE交CD延长线于点F,则S△EDF与S△BCF的比值是( )| A. | 1:2 | B. | 1:3 | C. | 1:4 | D. | 1:5 |
 如图所示,一把直尺和一块等腰直角三角板摆放在一起,则∠1+∠2=45°.
如图所示,一把直尺和一块等腰直角三角板摆放在一起,则∠1+∠2=45°.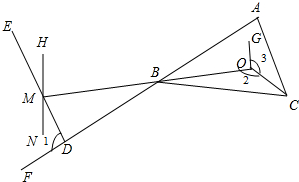 已知:如图,点D在射线AF上,AF与OM交于点B,DE交NH于点M,CA∥DE.
已知:如图,点D在射线AF上,AF与OM交于点B,DE交NH于点M,CA∥DE.