题目内容
11. 如图,在平行四边形ABCD中,点E为AD的中点,延长CE交BA的延长线于点F.
如图,在平行四边形ABCD中,点E为AD的中点,延长CE交BA的延长线于点F.(1)求证:AB=AF;
(2)若BC=2AB,∠BCD=110°,求∠ABE的度数.
分析 (1)由四边形ABCD是平行四边形,点E为AD的中点,易证得△DEC≌△AEF(AAS),继而可证得DC=AF,又由DC=AB,证得结论;
(2)由(1)可知BF=2AB,EF=EC,然后由∠BCD=110°求得BE平分∠CBF,继而求得答案.
解答 (1)证明:∵四边形ABCD是平行四边形,
∴CD=AB,CD∥AB,
∴∠DCE=∠F,∠FBC+∠BCD=180°,
∵E为AD的中点,
∴DE=AE.
在△DEC和△AEF中,
$\left\{\begin{array}{l}{∠DCE=∠F}\\{∠DEC=∠AEF}\\{DE=AE}\end{array}\right.$,
∴△DEC≌△AEF(AAS).
∴DC=AF.
∴AB=AF;
(2)解:由(1)可知BF=2AB,EF=EC,
∵∠BCD=110°,
∴∠FBC=180°-110°=70°,
∵BC=2AB,
∴BF=BC,
∴BE平分∠CBF,
∴∠ABE=$\frac{1}{2}$∠FBC=$\frac{1}{2}$×70°=35°.
点评 此题考查了平行四边形的性质、全等三角形的判定与性质以及等腰三角形的性质.注意证得△DEC≌△AEF与△BCF是等腰三角形是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.计算3-2的结果正确的是( )
| A. | $\frac{1}{9}$ | B. | -$\frac{1}{9}$ | C. | 9 | D. | -9 |
16.据统计,2015年长沙市的常住人口约为7500000人,将数据7500000用科学记数法表示为( )
| A. | 7.5×106 | B. | 0.75×107 | C. | 7.5×107 | D. | 75×105 |
3.下列运算正确的是( )
| A. | 2a3•a4=a12 | B. | 2$\sqrt{2}$×$\sqrt{2}$=4 | C. | (2a4)3=8a7 | D. | a8÷a2=a4 |
 当某一面积S关于某一线段x是一次函数时,则称S是关于x的奇特面积.如图,∠BAC=45°,点D在AC边上,且DA=2.点P,Q同时从D点出发,分别沿射线DC、射线DA运动,P点的运行速度是Q点的$\sqrt{2}$倍,当点Q到达A时,点P,Q同时停止运动.过点Q作AC的垂线段QR,使QR=PQ,连接PR.设QD=x,△PQR和∠BAC重叠部分的面积为S,请问S是否存在关于x的奇特面积?若存在,求奇特面积S关于x的函数关系式;若不存在,请说明理由.
当某一面积S关于某一线段x是一次函数时,则称S是关于x的奇特面积.如图,∠BAC=45°,点D在AC边上,且DA=2.点P,Q同时从D点出发,分别沿射线DC、射线DA运动,P点的运行速度是Q点的$\sqrt{2}$倍,当点Q到达A时,点P,Q同时停止运动.过点Q作AC的垂线段QR,使QR=PQ,连接PR.设QD=x,△PQR和∠BAC重叠部分的面积为S,请问S是否存在关于x的奇特面积?若存在,求奇特面积S关于x的函数关系式;若不存在,请说明理由.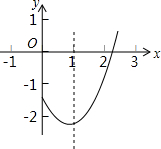 在平面直角坐标系中,抛物线y=ax2+bx+c(a,b,c是常数,a>0)的部分图象如图所示,直线x=1是它的对称轴.若一元二次方程ax2+bx+c=0的一个根x1的取值范围是2<x1<3,则它的另一个根x2的取值范围是-1<x2<0.
在平面直角坐标系中,抛物线y=ax2+bx+c(a,b,c是常数,a>0)的部分图象如图所示,直线x=1是它的对称轴.若一元二次方程ax2+bx+c=0的一个根x1的取值范围是2<x1<3,则它的另一个根x2的取值范围是-1<x2<0. 如图,四边形ABCD的顶点坐标A(-3,6)、B(-1,4)、C(-1,3)、D(-5,3).若四边形ABCD绕点C按顺时针方向旋转90°,再向左平移2个单位,得到四边形A′B′C′D′,则点A的对应点A′的坐标是( )
如图,四边形ABCD的顶点坐标A(-3,6)、B(-1,4)、C(-1,3)、D(-5,3).若四边形ABCD绕点C按顺时针方向旋转90°,再向左平移2个单位,得到四边形A′B′C′D′,则点A的对应点A′的坐标是( ) 折叠矩形ABCD,使点D落在BC边上的点F处,若折痕AE=5$\sqrt{5}$,tan∠EFC=$\frac{3}{4}$,则BC=10.
折叠矩形ABCD,使点D落在BC边上的点F处,若折痕AE=5$\sqrt{5}$,tan∠EFC=$\frac{3}{4}$,则BC=10.