Question

9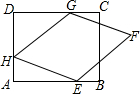．如图，矩形ABCD中，AD=6，DC=8，菱形EFGH的三个顶点E、G、H分別在矩形ABCD的边AB、CD、DA上，AH=2．
（1）已知DG=6，求AE的长；
（2）已知DG=2，求证：四边形EFGH为正方形．

Answer 1

分析 （1）先根据矩形的性质，利用勾股定理列出表达式：HG²=DH²+DG²，HE²=AH²+AE²，再根据菱形的性质，得到等式DH²+DG²=AH²+AE²，最后计算AE的长；
（2）先根据已知条件，用HL判定Rt△DHG≌Rt△AEH，得到菱形的一组邻边相等，进而判定该菱形为正方形．

解答 解：（1）∵AD=6，AH=2
∴DH=AD-AH=4
∵四边形ABCD是矩形
∴∠A=∠D=90°
∴在Rt△DHG中，HG²=DH²+DG²
在Rt△AEH中，HE²=AH²+AE²
∵四边形EFGH是菱形
∴HG=HE
∴DH²+DG²=AH²+AE²
即4²+6²=2²+AE²
∴AE=$\sqrt{48}$=4$\sqrt{3}$
（2）∵AH=2，DG=2
∴AH=DG
∵四边形EFGH是菱形
∴HG=HE
在Rt△DHG和Rt△AEH中
$\left\{\begin{array}{l}{HG=EH}\\{DG=AH}\end{array}\right.$
∴Rt△DHG≌Rt△AEH（HL）
∴∠DHG=∠AEH
∵∠AEH+∠AHE=90°
∴∠DHG+∠AHE=90°
∴∠GHE=90°
∵四边形EFGH是菱形
∴四边形EFGH是正方形

点评 本题主要考查了矩形、菱形的性质以及正方形的判定，解决问题的关键是掌握：矩形的四个角都是直角，菱形的四条边都线段，有一组邻边相等的菱形是正方形．在解题时注意，求直角三角形的边长时，一般都需要考虑运用勾股定理进行求解．