题目内容
6. 如图,在平行四边形ABCD中,过点B作BE⊥CD,垂足为E,连接AE,F为AE上一点,且∠BFE=∠C.
如图,在平行四边形ABCD中,过点B作BE⊥CD,垂足为E,连接AE,F为AE上一点,且∠BFE=∠C.(1)求证:△ABF∽△EAD;
(2)若AD=3,∠BAE=30°,求BF的长.(计算结果保留根号)
分析 (1)可通过证明∠BAF=∠AED,∠AFB=∠D,证得△ABF∽△EAD;
(2)根据平行线的性质得到BE⊥AB,根据三角函数的定义得到tan∠BAE=$\frac{AB}{EA}=\frac{\sqrt{3}}{2}$,根据相似三角形的性质即可得到结论.
解答 (1)证明:在平行四边形ABCD中,
∵∠D+∠C=180°,AB∥CD,
∴∠BAF=∠AED.
∵∠AFB+∠BFE=180°,∠D+∠C=180°,∠BFE=∠C,
∴∠AFB=∠D,
∴△ABF∽△EAD;
(2)解:∵BE⊥CD,AB∥CD,
∴BE⊥AB.
∴∠ABE=90°.
在Rt△ABE中,∠BAE=30°,
∴tan∠BAE=$\frac{AB}{EA}=\frac{\sqrt{3}}{2}$,
∵由(1)知,△ABF∽△EAD,
∴$\frac{AB}{EA}=\frac{BF}{AD}$,
∵AD=3,
∴BF=$\frac{3\sqrt{3}}{2}$.
点评 本题主要考查了相似三角形的判定和性质,同时也用到了平行四边形的性质和等角的补角相等等知识点.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
16.据统计,2015年长沙市的常住人口约为7500000人,将数据7500000用科学记数法表示为( )
| A. | 7.5×106 | B. | 0.75×107 | C. | 7.5×107 | D. | 75×105 |
17.一项“过关游戏”规定:在过第n关时要将一颗质地均匀的骰子(六个面上分别刻有1到6的点数)抛掷n次,若n次抛掷所出现的点数之和大于n2,则算过关;否则不算过关,则能过第二关的概率是( )
| A. | $\frac{15}{18}$ | B. | $\frac{5}{18}$ | C. | $\frac{11}{18}$ | D. | $\frac{9}{18}$ |
15.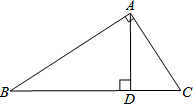 如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,则下列结论不正确的是( )
如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,则下列结论不正确的是( )
 如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,则下列结论不正确的是( )
如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,则下列结论不正确的是( )| A. | $sinB=\frac{AD}{AB}$ | B. | $sinB=\frac{AC}{BC}$ | C. | $sinB=\frac{AD}{AC}$ | D. | $sinB=\frac{CD}{AC}$ |

 折叠矩形ABCD,使点D落在BC边上的点F处,若折痕AE=5$\sqrt{5}$,tan∠EFC=$\frac{3}{4}$,则BC=10.
折叠矩形ABCD,使点D落在BC边上的点F处,若折痕AE=5$\sqrt{5}$,tan∠EFC=$\frac{3}{4}$,则BC=10.
 如图,用扳手拧螺母时,旋转中心为螺丝(母)的中心,旋转角为0°~360°的任意角(答案不唯一).
如图,用扳手拧螺母时,旋转中心为螺丝(母)的中心,旋转角为0°~360°的任意角(答案不唯一).