题目内容
某商店经销一种成本为每千克40元的水产品,据市场分析,若按每千克50元销售,一个月能售出500千克.若销售价每涨1元,则月销售量减少10千克.
(1)要使月销售利润达到最大,销售单价应定为多少元?
(2)要使月销售利润不低于8000元,请结合图象说明销售单价应如何定?
(1)要使月销售利润达到最大,销售单价应定为多少元?
(2)要使月销售利润不低于8000元,请结合图象说明销售单价应如何定?
考点:二次函数的应用
专题:
分析:(1)设销售单价定为每千克x元,获得利润为w元,则可以根据成本,求出每千克的利润,以及按照销售价每涨1元,月销售量就减少10千克,可求出销量.从而得到总利润关系式;
(2)先计算出y=8000时所对应的x的值,然后画出函数的大致图象,再根据图象回答即可.
(2)先计算出y=8000时所对应的x的值,然后画出函数的大致图象,再根据图象回答即可.
解答:解:(1)设销售单价定为每千克x元,获得利润为w元,则:
w=(x-40)[500-(x-50)×10],
=(x-40)(1000-10x),
=-10x2+1400x-40000,
=-10(x-70)2+9000,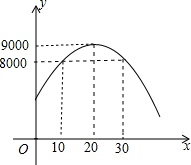
故当x=70时,利润最大为9000元.
答:要使月销售利润达到最大,销售单价应定为70元;
(2)令y=8000,则-10(x-20)2+9000=8000,
解得x1=10,x2=30.
函数的大致图象为:
观察图象当10≤x≤30时,y不低于8000.
所以当销售单价不小于60元而不大于80元时,商场获得的周销售利润不低于8000元.
w=(x-40)[500-(x-50)×10],
=(x-40)(1000-10x),
=-10x2+1400x-40000,
=-10(x-70)2+9000,

故当x=70时,利润最大为9000元.
答:要使月销售利润达到最大,销售单价应定为70元;
(2)令y=8000,则-10(x-20)2+9000=8000,
解得x1=10,x2=30.
函数的大致图象为:
观察图象当10≤x≤30时,y不低于8000.
所以当销售单价不小于60元而不大于80元时,商场获得的周销售利润不低于8000元.
点评:本题主要考查了二次函数的应用,能正确表示出月销售量是解题的关键.求二次函数的最大(小)值有三种方法,第一种可由图象直接得出,第二种是配方法,第三种是公式法,常用的是后两种方法.

练习册系列答案
相关题目
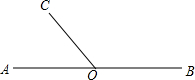 如图,点O为直线AB上一点,∠AOC=50°.
如图,点O为直线AB上一点,∠AOC=50°. 如图,点B、D、C是⊙A上的点,∠BDC=130°,则∠BAC=
如图,点B、D、C是⊙A上的点,∠BDC=130°,则∠BAC=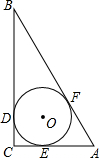 如图,在Rt△ABC中,∠C=90°,AC=5cm,BC=12cm.
如图,在Rt△ABC中,∠C=90°,AC=5cm,BC=12cm. 某小区有100个停车位,给业主停车带来了方便,去年1-6月,每个车位租价y为360元,7-12月,每个车位租价y(元)与月份x关系如表所示.去年1-12月,每月租出车位m(个)与月份x关系如图.已知业主只需支付月租给物管公司,公司每月每车位需支付管理费p=6x(1≤x≤12,x取整数).
某小区有100个停车位,给业主停车带来了方便,去年1-6月,每个车位租价y为360元,7-12月,每个车位租价y(元)与月份x关系如表所示.去年1-12月,每月租出车位m(个)与月份x关系如图.已知业主只需支付月租给物管公司,公司每月每车位需支付管理费p=6x(1≤x≤12,x取整数).