题目内容
一项工程甲独做10天完成,乙独做15天完成,丙独做20天完成.开始三队合作,后甲队调做其它工作,由乙、丙两队合作,全部工作共用6天.若设甲队参加了x天,求甲队参加的天数,则可列方程 .
考点:由实际问题抽象出一元一次方程
专题:
分析:把这项工程的工作总量看作1,设甲队参加了x天,求得甲队完成的工作量,再根据乙、丙两队合作,全部工作共用6天.求得乙、丙完成的工作量,根据工作量的和为1,列出方程即可.
解答:解:设甲队参加了x天,由题意得
x+6×(
+
)=1.
故答案为:
x+6×(
+
)=1.
| 1 |
| 10 |
| 1 |
| 15 |
| 1 |
| 20 |
故答案为:
| 1 |
| 10 |
| 1 |
| 15 |
| 1 |
| 20 |
点评:此题考查从实际问题中抽出一元一次方程,掌握工作总量、工作时间、工作效率三者之间的数量关系是解决问题的关键.

练习册系列答案
相关题目
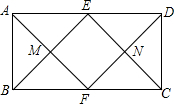 如图,在矩形ABCD中,E,F分别是AD,BC中点,连接AF,BE,CE,DF分别交于点M,N,四边形EMFN是( )
如图,在矩形ABCD中,E,F分别是AD,BC中点,连接AF,BE,CE,DF分别交于点M,N,四边形EMFN是( )| A、正方形 | B、菱形 |
| C、矩形 | D、无法确定 |