题目内容
已知△ABC中,∠BAC=∠ABC=22.5°,AC=
,求S△ABC.
| 6 |
考点:等腰直角三角形,等腰三角形的性质
专题:
分析:过B作BD⊥AC延长线于点D,易证AC=BC,∠BCD=45°,即可判定△BCD是等腰直角三角形,即可求得BD的值,即可解题.
解答:解:过B作BD⊥AC延长线于点D,

∵∠BAC=∠ABC=22.5°,
∴∠BCD=45°,AC=BC,
∴△BCD是等腰直角三角形,
∴BD=
BC=
,
∴S△ABC=
AC•BD=
×
×
=
.

∵∠BAC=∠ABC=22.5°,
∴∠BCD=45°,AC=BC,
∴△BCD是等腰直角三角形,
∴BD=
| ||
| 2 |
| 3 |
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 6 |
| 3 |
3
| ||
| 2 |
点评:本题考查了等腰直角三角形的性质,考查了三角形面积的计算,本题中判定△BCD是等腰直角三角形是解题的关键.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
下面的计算正确的是( )
| A、3x2•4x2=12x2 |
| B、(xy5)3=xy15 |
| C、x4÷x=x3 |
| D、(x5)2=x2 |
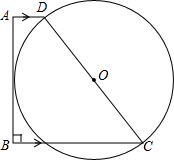 已知,如图,ABCD为直角梯形,AB⊥BC,CD=AD+BC,
已知,如图,ABCD为直角梯形,AB⊥BC,CD=AD+BC,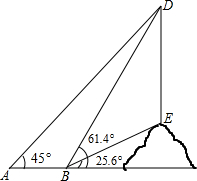 如图,课外数学小组要测量小山坡上塔的高度DE,DE所在直线与水平线AN垂直.他们在A处测得塔尖D的仰角为45°,再沿着射线AN方向前进50米到达B处,此时测得塔尖D的仰角∠DBN=25.6°.现在请你帮助课外活动小组算一算塔高DE大约是多少米?(结果精确到个位)(参考数据:sin25.6°≈0.4,cos25.6°≈0.9,tan25.6°≈0.5,sin61.4°≈0.9,cos61.4°≈0.5,tan61.4°≈1.8)
如图,课外数学小组要测量小山坡上塔的高度DE,DE所在直线与水平线AN垂直.他们在A处测得塔尖D的仰角为45°,再沿着射线AN方向前进50米到达B处,此时测得塔尖D的仰角∠DBN=25.6°.现在请你帮助课外活动小组算一算塔高DE大约是多少米?(结果精确到个位)(参考数据:sin25.6°≈0.4,cos25.6°≈0.9,tan25.6°≈0.5,sin61.4°≈0.9,cos61.4°≈0.5,tan61.4°≈1.8)