题目内容
已知直线y=-
x+6和双曲线y=
(k>0)在第一象限内交于两点A,B,
(1)求实数k的取值范围;
(2)若△AOB的面积S为12,求k的值.
| 3 |
| 4 |
| x |
| k |
(1)求实数k的取值范围;
(2)若△AOB的面积S为12,求k的值.
考点:反比例函数与一次函数的交点问题
专题:
分析:(1)由于直线y=-
x+6与与双曲线y=
在第一象限交于两点A,B,则方程组
有两组解,消去y得到关于x的一元二次方程,根据判别式的意义得到△>0,解得k的范围,根据反比例函数k>0,于是得到k的取值范围;
(2)设直线y=-
x+6与x,y轴分别交与点C,D,根据S△AOB=S△COD-S△AOD-S△BOC,可得出k的值.
| 3 |
| 4 |
| x |
| k |
|
(2)设直线y=-
| 3 |
| 4 |
解答: 解:(1)∵直线y=-
解:(1)∵直线y=-
x+6与与双曲线y=
在第一象限交于两点A,B,
∴A(
,
+3),B(
,-
+3),
∴方程组
有两组解,
∴关于x的一元二次方程3x2-24x+4k=0的判别式△=(-24)2-4•3•4k>0,
解得k<12,
∵k>0,
∴k的取值范围为0<k<12.
(2)设直线y=-
x+6与x,y轴分别交与点C,D,
∴C(8,0),D(0,6),
∵S△AOB=S△COD-S△AOD-S△BOC,
∴12=
×6×8-
×6×
-
×8×(-
+3),
整理得
=3,
解得k=9.
 解:(1)∵直线y=-
解:(1)∵直线y=-| 3 |
| 4 |
| x |
| k |
∴A(
12-2
| ||
| 3 |
| ||
| 2 |
12+2
| ||
| 3 |
| ||
| 2 |
∴方程组
|
∴关于x的一元二次方程3x2-24x+4k=0的判别式△=(-24)2-4•3•4k>0,
解得k<12,
∵k>0,
∴k的取值范围为0<k<12.
(2)设直线y=-
| 3 |
| 4 |
∴C(8,0),D(0,6),
∵S△AOB=S△COD-S△AOD-S△BOC,
∴12=
| 1 |
| 2 |
| 1 |
| 2 |
12-2
| ||
| 3 |
| 1 |
| 2 |
| ||
| 2 |
整理得
| 36-3k |
解得k=9.
点评:本题考查了反比例函数与一次函数的交点问题:求反比例函数与一次函数的交点坐标,把两个函数关系式联立成方程组求解,若方程组有解则两者有交点,方程组无解,则两者无交点.

练习册系列答案
相关题目
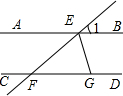 如图,AB∥CD,EF交AB、CD于点E、F、EG平分∠BEF,交CD于点G.若∠1=40°,则∠EGF=( )
如图,AB∥CD,EF交AB、CD于点E、F、EG平分∠BEF,交CD于点G.若∠1=40°,则∠EGF=( )| A、20° | B、40° |
| C、70° | D、110° |
下面的计算正确的是( )
| A、3x2•4x2=12x2 |
| B、(xy5)3=xy15 |
| C、x4÷x=x3 |
| D、(x5)2=x2 |
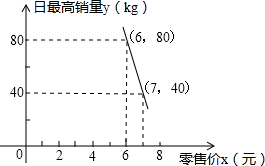 某水果经销商到水果批发市场批发某种水果时了解到如下行情:每千克水果的批发价为4元,经调查,经销商销售该水果的日最高销量与零售价之间的函数关系如图中直线AB所示,该经销商准备购进一定量的水果,且在销售时当日零售价保持不变,考虑到保鲜水果要增加成本,因此经销商要确保每天批发进来的水果全部售完.
某水果经销商到水果批发市场批发某种水果时了解到如下行情:每千克水果的批发价为4元,经调查,经销商销售该水果的日最高销量与零售价之间的函数关系如图中直线AB所示,该经销商准备购进一定量的水果,且在销售时当日零售价保持不变,考虑到保鲜水果要增加成本,因此经销商要确保每天批发进来的水果全部售完.