题目内容
19.把一个矩形减去一个正方形,若所剩下的矩形与原矩形相似,原矩形长边与正方形的边长之比等于( )| A. | (1+$\sqrt{5}$):2 | B. | 3:2 | C. | (1+$\sqrt{3}$):2 | D. | (1+$\sqrt{6}$):2 |
分析 根据相似多边形的性质列出比例式,根据正方形的性质代入计算即可.
解答 解: ∵矩形ABFE∽矩形ABCD,
∵矩形ABFE∽矩形ABCD,
∴$\frac{AE}{AB}$=$\frac{AB}{AD}$,即$\frac{AD-AB}{AB}$=$\frac{AB}{AD}$,
整理得,AD2-AB•AD-AB2=0
两边同除AB2得,($\frac{AD}{AB}$)2-$\frac{AD}{AB}$-1=0,
解得$\frac{AD}{AB}$=$\frac{1±\sqrt{5}}{2}$,
负数不合题意,
∴$\frac{AD}{AB}$=$\frac{1+\sqrt{5}}{2}$.
故选:A.
点评 本题考查的是相似多边形的性质,掌握相似多边形的对应边成比例是解题的关键.

练习册系列答案
相关题目
11.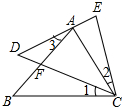 如图,DE经过点A,∠1=∠2=∠3,AC=CE,则下列依据①SAS,②ASA,③AAS,④AAA中,能判定△ABC≌△EDC的是( )
如图,DE经过点A,∠1=∠2=∠3,AC=CE,则下列依据①SAS,②ASA,③AAS,④AAA中,能判定△ABC≌△EDC的是( )
 如图,DE经过点A,∠1=∠2=∠3,AC=CE,则下列依据①SAS,②ASA,③AAS,④AAA中,能判定△ABC≌△EDC的是( )
如图,DE经过点A,∠1=∠2=∠3,AC=CE,则下列依据①SAS,②ASA,③AAS,④AAA中,能判定△ABC≌△EDC的是( )| A. | ①和② | B. | ②和④ | C. | ②和③ | D. | ①和③ |