题目内容
7.在三角形ABC中,三边长分别是AB=5、AC=12、BC=13,则BC边上的高AD=$\frac{60}{13}$.分析 根据勾股定理逆定理可证明△ABC是直角三角形,再利用直角三角形的面积公式可得$\frac{1}{2}×5×12$=$\frac{1}{2}×13$×AD,解可得答案.
解答 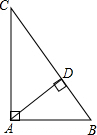 解:∵52+122=132,
解:∵52+122=132,
∴AB2+AC2=BC2,
∴△ABC是直角三角形,
S△ABC=$\frac{1}{2}$AB•AC=$\frac{1}{2}$BC•AD,
$\frac{1}{2}×5×12$=$\frac{1}{2}×13$×AD,
∴AD=$\frac{60}{13}$,
故答案为:$\frac{60}{13}$.
点评 此题主要考查了勾股定理逆定理,关键是掌握如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形.

练习册系列答案
相关题目
2.已知反比例函数y=$\frac{-2}{x}$的图象上有两点A(-2、y1)、B、(-1,y2),则y1、-y2的值是( )
| A. | 正数 | B. | 负数 | C. | 非正数 | D. | 不得确定 |
12.已知抛物线的解析式为y=(2x+1)2-2,则抛物线的顶点坐标为( )
| A. | (-1,-2) | B. | (1,-2) | C. | (-$\frac{1}{2}$,-2) | D. | ($\frac{1}{2}$,-2) |
19.把一个矩形减去一个正方形,若所剩下的矩形与原矩形相似,原矩形长边与正方形的边长之比等于( )
| A. | (1+$\sqrt{5}$):2 | B. | 3:2 | C. | (1+$\sqrt{3}$):2 | D. | (1+$\sqrt{6}$):2 |
 怎样移动A、B、C中的两点,才能使三个点表示的数相同?有几种移法?
怎样移动A、B、C中的两点,才能使三个点表示的数相同?有几种移法?