题目内容
 如图,Rt△ABC中,∠C=90°,将△ABC沿AB向下翻折后,再绕点A按顺时针方向旋转α度(α<∠BAC),得到Rt△ADE,其中斜边AE交BC于点F,直角边DE分别交AB、BC于点G、H.
如图,Rt△ABC中,∠C=90°,将△ABC沿AB向下翻折后,再绕点A按顺时针方向旋转α度(α<∠BAC),得到Rt△ADE,其中斜边AE交BC于点F,直角边DE分别交AB、BC于点G、H.(1)求证:∠AFC=∠AGD;
(2)求证:△AFB≌△AGE.
考点:全等三角形的判定与性质,翻折变换(折叠问题),旋转的性质
专题:证明题
分析:(1)由折叠的性质得到三角形ABC与三角形AED全等,利用全等三角形的对应边相等,对应角相等得到AC=AD,∠BAC=∠EAD,进而得到∠FAC=∠GAD,利用等角的余角相等即可得证;
(2)由题意得到AB=AE,∠ABC=∠E,再由一对公共角相等,利用ASA即可得证.
(2)由题意得到AB=AE,∠ABC=∠E,再由一对公共角相等,利用ASA即可得证.
解答:证明:(1)由题意得:△ABC≌△AED,
∴AC=AD,∠BAC=∠EAD,
∴∠BAC-∠EAB=∠EAD-∠EAB,即∠FAC=∠GAD,
在Rt△AFC和Rt△AGD中,
则∠AFC=90°-∠FAC=90°-∠GAD=∠AGD;
(2)由题意得AB=AE,∠ABC=∠E,
在△AFB和△AGE中,
,
∴△AFB≌△AGE(ASA).
∴AC=AD,∠BAC=∠EAD,
∴∠BAC-∠EAB=∠EAD-∠EAB,即∠FAC=∠GAD,
在Rt△AFC和Rt△AGD中,
则∠AFC=90°-∠FAC=90°-∠GAD=∠AGD;
(2)由题意得AB=AE,∠ABC=∠E,
在△AFB和△AGE中,
|
∴△AFB≌△AGE(ASA).
点评:此题考查了全等三角形的判定与性质,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
 学习实践园地系列答案
学习实践园地系列答案
相关题目
 如图,直线AB与x轴交于点A(2,0),与y轴交于B点,并且△AOB的面积为3.
如图,直线AB与x轴交于点A(2,0),与y轴交于B点,并且△AOB的面积为3.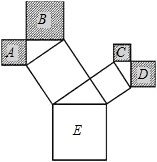 如图是勾股树的一部分,在一个正方形上以正方形的边为边长,构造直角三角形,再以直角边为边长作正方形,不断重复同个过程.设图中最大的正方形边长为5,正方形A,B,C,D,E的面积和为S,求S的值.
如图是勾股树的一部分,在一个正方形上以正方形的边为边长,构造直角三角形,再以直角边为边长作正方形,不断重复同个过程.设图中最大的正方形边长为5,正方形A,B,C,D,E的面积和为S,求S的值. (1)解不等式并把不等式的解表示在数轴上:
(1)解不等式并把不等式的解表示在数轴上: AB是圆O的直径,AC是圆O的切线,BC与圆O相交于点D,点E在圆O上,且DE=DA,AE与BC相交于点F,求证:FD=DC.
AB是圆O的直径,AC是圆O的切线,BC与圆O相交于点D,点E在圆O上,且DE=DA,AE与BC相交于点F,求证:FD=DC. 如图,直线y=kx+m与y=-x+b相交于P点,则不等式组
如图,直线y=kx+m与y=-x+b相交于P点,则不等式组