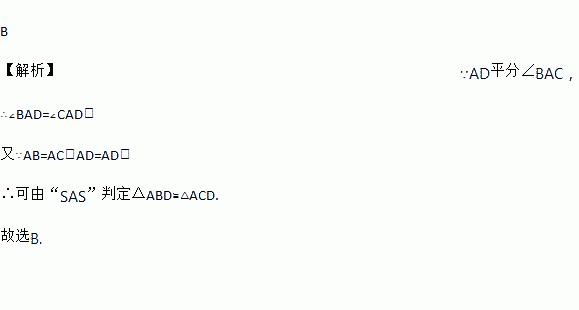题目内容
如图，AD平分∠BAC，AB=AC，那么判定△ABD≌△ACD的理由是（ ）
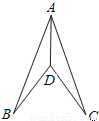
A. SSS B. SAS C. ASA D. AAS
B
【解析】∵AD平分∠BAC，
∴∠BAD=∠CAD，
又∵AB=AC，AD=AD，
∴可由“SAS”判定△ABD≌△ACD.
故选B.
计算：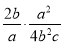 
＝________
【解析】试题解析：
故答案为： 两人比赛读一本科普读物共98页，王力读了一周（7天）还没有读完，而张勇不到一周就读完了．张勇平均每天比王力多读3页，王力平均每天读__页．（答案取整数）
12或13
【解析】【解析】
设王力平均每天读x页，则张勇平均每天读（x+3）页．根据题意得：
，解得：11＜x＜14．
∵x取整数，∴x=12或x=13．
故答案为：12或13． 若
x2m－1－8＞5是一元一次不等式，则m的值为( )
A. 0 B. 1
C. 2 D. 3
B
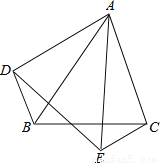
【解析】根据一元一次不等式的定义得： ，故选B. 如图，△ABC和△AED中，∠BAC=∠DAE，AB=AE，AC=AD，连接BD、CE，求证：BD=EC。
证明见解析
【解析】试题分析：
由∠BAC=∠DAE易得∠BAD=∠EAC，结合AB=AE，AC=AD，即可由“SAS”证得：△BAD≌△EAC，从而可得：BD=EC.
试题解析：
∵∠DAE=∠BAC，
∴∠DAE-∠BAE=∠EAC-∠BAE，
∴∠BAD=∠EAC，
在△BAD和△EAC中，
∴△BAD≌△EAC（SAS），
∴BD=EC... 甲、乙两商场以同样价格出售同样的商品，并且又各自推出不同的优惠方案：在甲商场累计购物超过100元后，超出100元的部分按90%收费；在乙商场累计购物超过50元后，超出50元的部分按95%收费，设小红在同一商场累计购物x元，其中x＞100．
（1）根据题意，填写下表（单位：元）；
累计购物 实际花费 | 130 | 290 | … | x |
在甲商场 | 127 |
| … |
|
在乙商场 | 126 |
| … |
|
（2）当x取何值时，小红在甲、乙两商场的实际花费相同？
（3）当小红在同一商场累计购物超过100元时，在哪家商场的实际花费少？
（1）在甲商场：100+（290﹣100）×0.9=271，100+（x﹣100）×0.9=0.9x+10；
在乙商场：50+（290﹣50）×0.95=278，50+（x﹣50）×0.95=0.95x+2.5；
（2）当x为150时，小红在甲、乙两商场的实际花费相同；
（3）当小红累计购物超过100元而不到150元时，在乙商场实际花费少；正好为150元时，两商场花费相同；大于1... 小美将某服饰店的促销活动内容告诉小明后，小明假设某一商品的定价为x元，并列出关系式为0.3（2x-100）＜1000，则下列何者可能是小美告诉小明的内容？（ ）
A. 买两件等值的商品可减100元，再打3折，最后不到1000元
B. 买两件等值的商品可减100元，再打7折，最后不到1000元
C. 买两件等值的商品可打3折，再减100元，最后不到1000元
D. 买两件等值的商品可打7折，再减100元，最后不到1000元
A
【解析】【解析】
由关系式可知：
0.3（2x﹣100）＜1000，
由2x﹣100，得出两件商品减100元，以及由0.3（2x﹣100）得出买两件打3折，
故可以理解为：买两件等值的商品可减100元，再打3折，最后不到1000元．
故选A． 不等式组﹣1＜x＜4的整数解有_________个．
4
【解析】在﹣1＜x＜4范围内的整数只有0，1，2，3，
所以等式﹣1＜x＜4的整数解有4个，
故答案为4． 如图，在?ABCD中，点E，F在对角线AC上，且AE=CF．求证：
（1）DE=BF；
（2）四边形DEBF是平行四边形．
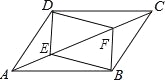
详见解析.
【解析】
试题分析：（1）根据全等三角形的判定方法，判断出△ADE≌△CBF，即可推得DE=BF．（2）首先判断出DE∥BF；然后根据一组对边平行且相等的四边形是平行四边形，推得四边形DEBF是平行四边形即可．
试题解析：（1）∵四边形ABCD是平行四边形，
∴AD∥CB，AD=CB，
∴∠DAE=∠BCF，
在△ADE和△CBF中，
∴△AD...