题目内容
15.当k>3时,关于x的方程2x+3=k的解为正数.分析 将k看做常数解方程得x=$\frac{k-3}{2}$,根据方程的解为正数得出关于k的不等式,解之可得.
解答 解:移项,得:2x=k-3,
系数化为1,得:x=$\frac{k-3}{2}$,
根据题意可得$\frac{k-3}{2}$>0,
解得:k>3,
故答案为:>3.
点评 本题主要考查解一元一次方程和一元一次不等式的能力,解题的关键是根据题意得到关于k的不等式.

练习册系列答案
相关题目
3.在等腰直角三角形ABC中,斜边AB=2$\sqrt{2}$cm,则三角形ABC的面积等于( )
| A. | 2cm2 | B. | 4cm2 | C. | $\sqrt{2}$cm2 | D. | 2$\sqrt{2}$cm2 |
7.若x<2,化简$\sqrt{(x-2)^{2}}$+|3-x|的正确结果是( )
| A. | -1 | B. | 1 | C. | 2x-5 | D. | 5-2x |
4.下列计算正确的是( )
| A. | $\sqrt{3}+\sqrt{2}=\sqrt{5}$ | B. | $\sqrt{2}×\sqrt{5}=\sqrt{10}$ | C. | $\sqrt{8}-\sqrt{2}=\sqrt{6}$ | D. | $\sqrt{8}÷\sqrt{2}=4$ |
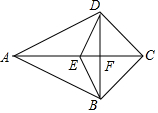 如图,在四边形ABCD中,AC与BD相交于点F,E为AC上一点,且AD=AB,ED=EB.
如图,在四边形ABCD中,AC与BD相交于点F,E为AC上一点,且AD=AB,ED=EB.