Question

5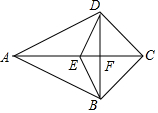．如图，在四边形ABCD中，AC与BD相交于点F，E为AC上一点，且AD=AB，ED=EB．
（1）说明△AED与△AEB全等的理由；
（2）说明△EBF与△EDF全等的理由．

Answer 1

分析 （1）直接利用全等三角形的判定方法进而得出△AED≌△AEB（SSS）；
（2）直接利用全等三角形的判定方法进而得出△EBF≌△EDF（SAS）．

解答 证明：（1）在△AED和△AEB中
∵$\left\{\begin{array}{l}{AD=AB}\\{AE=AE}\\{DE=BE}\end{array}\right.$，
∴△AED≌△AEB（SSS）；

（2）∵△AED≌△AEB，
∴∠AED=∠AEB，
∴∠DEF=∠BEF，
在△EBF和△EDF中
∵$\left\{\begin{array}{l}{DE=EB}\\{∠DEF=∠BEF}\\{EF=EF}\end{array}\right.$，
∴△EBF≌△EDF（SAS）．

点评 此题主要考查了全等三角形的判定和性质的应用，注意：全等三角形的判定定理有SAS，ASA，AAS，SSS．