题目内容
下列条件中,不能判断ABC为直角三角形的是( )
| A、a=3,b=4,c=5 |
| B、∠A+∠B=∠C |
| C、a=1,b=2,c=3 |
| D、∠A:∠B:∠C=1:2:3 |
考点:勾股定理的逆定理,三角形内角和定理
专题:计算题
分析:利用勾股定理的逆定理判断即可得到结果.
解答:解:A、∵a=3,b=4,c=5,即a2+b2=9+16=25,c2=25,
∴a2+b2=c2,
即△ABC为直角三角形,不合题意;
B、∵∠A+∠B=∠C,∠A+∠B+∠C=180°,
∴∠C=90°,即△ABC为直角三角形,不合题意;
C、∵a=1,b=2,c=3,即a2+b2=1+4=5,c2=9,
∴a2+b2≠c2,
即△ABC不是直角三角形,符合题意;
D、由∠A:∠B:∠C=1:2:3,得到∠A=x,∠B=2x,∠C=3x,
根据题意得:x+2x+3x=180°,即x=30°,
∴∠A=30°,∠B=60°,∠C=90°,不合题意.
故选C,
∴a2+b2=c2,
即△ABC为直角三角形,不合题意;
B、∵∠A+∠B=∠C,∠A+∠B+∠C=180°,
∴∠C=90°,即△ABC为直角三角形,不合题意;
C、∵a=1,b=2,c=3,即a2+b2=1+4=5,c2=9,
∴a2+b2≠c2,
即△ABC不是直角三角形,符合题意;
D、由∠A:∠B:∠C=1:2:3,得到∠A=x,∠B=2x,∠C=3x,
根据题意得:x+2x+3x=180°,即x=30°,
∴∠A=30°,∠B=60°,∠C=90°,不合题意.
故选C,
点评:此题考查了勾股定理的逆定理,熟练掌握勾股定理的逆定理是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,函数y=2x+2的图象与直线y=kx的交点横坐标为-
如图,函数y=2x+2的图象与直线y=kx的交点横坐标为-| 1 |
| 2 |
| A、x>-1 | ||
| B、x<-1 | ||
C、x>-
| ||
D、x<-
|
 如图,∠ACD=20°,DA=DB=DC,则∠ABC=( )
如图,∠ACD=20°,DA=DB=DC,则∠ABC=( )| A、50° | B、60° |
| C、70° | D、80° |
 小明拿一张如图的直角三角形纸片ABC,其中∠C=90°,他将纸片沿DE折叠,使点B与点A重合,∠CAD:∠BAD=5:2,则∠CDA的度数( )
小明拿一张如图的直角三角形纸片ABC,其中∠C=90°,他将纸片沿DE折叠,使点B与点A重合,∠CAD:∠BAD=5:2,则∠CDA的度数( )| A、20° | B、40° |
| C、50° | D、70° |
 如图,一枚棋子放在七边形A1A2A3A4A5A6A7的顶点A1处,现以逆时针方向沿着七边形的边移动这枚棋子,且规定:第一步从点A1处移动到A2处,第二步从点A2处移动到点A4处(在点A3处不停留),第三步从点A4处移动到AA7处(在点A5、A6处不停留),…,依此类推,若这枚棋子不停地这样一对下去,则这枚棋子永远不能停留的顶点有( )
如图,一枚棋子放在七边形A1A2A3A4A5A6A7的顶点A1处,现以逆时针方向沿着七边形的边移动这枚棋子,且规定:第一步从点A1处移动到A2处,第二步从点A2处移动到点A4处(在点A3处不停留),第三步从点A4处移动到AA7处(在点A5、A6处不停留),…,依此类推,若这枚棋子不停地这样一对下去,则这枚棋子永远不能停留的顶点有( )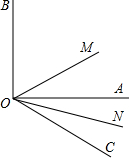 如图,∠AOB是直角,∠AOC=30°,ON是∠AOC的平分线,OM是∠BOC的平分线,求∠MON的度数.
如图,∠AOB是直角,∠AOC=30°,ON是∠AOC的平分线,OM是∠BOC的平分线,求∠MON的度数.