题目内容
如图,已知抛物线y=ax2+bx-4与x轴交于A(-2,0),B(8,0)两点,与y轴交于点C,连接BC,以BC为一边,作菱形BDEC,使其对角线在坐标轴上,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P作x轴的垂线l交抛物线于点Q.
(1)求抛物线的解析式;
(2)将抛物线向上平移n个单位,使其顶点在菱形BDEC内(不含菱形的边),求n的取值范围;
(3)当点P在线段OB上运动时,直线l交BD于点M.试探究m为何值时,四边形CQMD是平行四边形,并说明理由.

(1)求抛物线的解析式;
(2)将抛物线向上平移n个单位,使其顶点在菱形BDEC内(不含菱形的边),求n的取值范围;
(3)当点P在线段OB上运动时,直线l交BD于点M.试探究m为何值时,四边形CQMD是平行四边形,并说明理由.

考点:二次函数综合题
专题:
分析:(1)根据待定系数法即可求得.
(2)先求得直线BC的解析式和抛物线的顶点坐标G(3,-
),然后把x=3代入直线BC的解析式即可求得F的坐标,进而求得E的坐标即可求得n的取值.
(3)由菱形的对称性可知,点D的坐标,根据待定系数法可求直线BD的解析式,根据平行四边形的性质可得关于m的方程,求得m的值;再根据平行四边形的判定可得四边形CQBM的形状;
(2)先求得直线BC的解析式和抛物线的顶点坐标G(3,-
| 25 |
| 4 |
(3)由菱形的对称性可知,点D的坐标,根据待定系数法可求直线BD的解析式,根据平行四边形的性质可得关于m的方程,求得m的值;再根据平行四边形的判定可得四边形CQBM的形状;
解答:解:(1)∵抛物线y=ax2+bx-4与x轴交于A(-2,0),B(8,0)两点,
∴
解得
∴抛物线的解析式为:y=
x2-
x-4;

(2)设抛物线的顶点为G,过G点作x轴的垂线交BD于E,交BC于F,
由抛物线的解析式y=
x2-
x-4可知C(0,-4)
设直线BC的解析式为y=k1x+b1,
∵B(8,0),C(0,-4),则
,
解得k1=
,b1=-4.
故直线BC的解析式为y=
x-4.
∵y=
x2-
x-4=
(x-3)2-
,
∴抛物线的顶点G的坐标(3,-
),
当x=3时,y=
x-4=-
,
∴F(3,-
),
由菱形的对称性可知,点E的坐标为(3,
).
∵GF=-
-(-
)=
,GE=
-(-
)=
,
∴
<n<
.

(3)∵C(0,-4)
∴由菱形的对称性可知,点D的坐标为(0,4).
设直线BD的解析式为y=kx+b,则
,
解得k=-
,b=4.
∴直线BD的解析式为y=-
x+4.
∵l⊥x轴,
∴点M的坐标为(m,-
m+4),点Q的坐标为(m,
m2-
m-4).
如图,当MQ=DC时,四边形CQMD是平行四边形,
∴(-
m+4)-(
m2-
m-4)=4-(-4).
化简得:m2-4m=0,
解得m1=0(不合题意舍去),m2=4.
∴当m=4时,四边形CQMD是平行四边形.
∴
|
|
∴抛物线的解析式为:y=
| 1 |
| 4 |
| 3 |
| 2 |

(2)设抛物线的顶点为G,过G点作x轴的垂线交BD于E,交BC于F,
由抛物线的解析式y=
| 1 |
| 4 |
| 3 |
| 2 |
设直线BC的解析式为y=k1x+b1,
∵B(8,0),C(0,-4),则
|
解得k1=
| 1 |
| 2 |
故直线BC的解析式为y=
| 1 |
| 2 |
∵y=
| 1 |
| 4 |
| 3 |
| 2 |
| 1 |
| 4 |
| 25 |
| 4 |
∴抛物线的顶点G的坐标(3,-
| 25 |
| 4 |
当x=3时,y=
| 1 |
| 2 |
| 5 |
| 2 |
∴F(3,-
| 5 |
| 2 |
由菱形的对称性可知,点E的坐标为(3,
| 5 |
| 2 |
∵GF=-
| 5 |
| 2 |
| 25 |
| 4 |
| 15 |
| 4 |
| 5 |
| 2 |
| 25 |
| 4 |
| 35 |
| 4 |
∴
| 15 |
| 4 |
| 35 |
| 4 |

(3)∵C(0,-4)
∴由菱形的对称性可知,点D的坐标为(0,4).
设直线BD的解析式为y=kx+b,则
|
解得k=-
| 1 |
| 2 |
∴直线BD的解析式为y=-
| 1 |
| 2 |
∵l⊥x轴,
∴点M的坐标为(m,-
| 1 |
| 2 |
| 1 |
| 4 |
| 3 |
| 2 |
如图,当MQ=DC时,四边形CQMD是平行四边形,
∴(-
| 1 |
| 2 |
| 1 |
| 4 |
| 3 |
| 2 |
化简得:m2-4m=0,
解得m1=0(不合题意舍去),m2=4.
∴当m=4时,四边形CQMD是平行四边形.
点评:本题考查了二次函数综合性,涉及的知识点有:坐标轴上点的特点,菱形的对称性,待定系数法求直线的解析式,平行四边形的判定和性质,方程思想和分类思想的运用,综合性较强,有一定的难度.

练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
下列条件中,不能判断ABC为直角三角形的是( )
| A、a=3,b=4,c=5 |
| B、∠A+∠B=∠C |
| C、a=1,b=2,c=3 |
| D、∠A:∠B:∠C=1:2:3 |
 如图,四边形ABCD是直角梯形,AD∥BC,∠B=90°,AB=8cm,AD=24cm.BC=26cm,点P从点A出发,以1cm/s的速度向点D运动,点Q从点C同时出发,以3cm/s的速度向点B运动,其中一个动点到达端点时,另一个动点也随之停止运动.设运动的时间为t(秒).
如图,四边形ABCD是直角梯形,AD∥BC,∠B=90°,AB=8cm,AD=24cm.BC=26cm,点P从点A出发,以1cm/s的速度向点D运动,点Q从点C同时出发,以3cm/s的速度向点B运动,其中一个动点到达端点时,另一个动点也随之停止运动.设运动的时间为t(秒). 夏天到了,欣欣服装店老板用4500元购进一批卡通团T桖衫,由于深受顾客喜爱,很快售完,老板又用5000元购进第二批该款式T恤杉,所购数量与第一批相同,但每件进价比第一批多了10元.
夏天到了,欣欣服装店老板用4500元购进一批卡通团T桖衫,由于深受顾客喜爱,很快售完,老板又用5000元购进第二批该款式T恤杉,所购数量与第一批相同,但每件进价比第一批多了10元.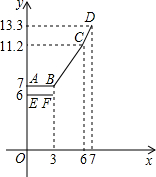 为缓解油价上涨给出租车行业带来的成本压力,某市自2007年11月17日起,调整出租车运价,调整方案见下列表格及图象(其中a,b,c为常数)
为缓解油价上涨给出租车行业带来的成本压力,某市自2007年11月17日起,调整出租车运价,调整方案见下列表格及图象(其中a,b,c为常数)