题目内容
4.如图所示是一个长为2m,款为2n的长方形,沿图中虚线用剪刀均分成四个完全相同的小长方形,然后按图的方式拼成一个正方形.(1)你认为图②中的阴影部分的正方形的边长等于m-n
(2)请你用两种不同的方式列代数式表示图②中阴影部分的面积.
方法①(m-n)2
方法②(m+n)2-4mn
(3)观察图②,写出(m+n)2,(m-n)2,mn这三个代数式之间的等量关系:(m-n)2=(m+n)2-4mn
(4)根据(3)题中的等量关系,解决问题:已知m+n=5,mn=4,求阴影部分正方形的边长.

分析 (1)根据线段的和差,可得答案;
(2)①根据正方形的面积公式,②根据面积的和差,可得答案;
(3)根据面积相等,可得答案;
(4)根据间接求面积的方法,可得答案.
解答 解:(1)你认为图②中的阴影部分的正方形的边长等于 m-n
(2)请你用两种不同的方式列代数式表示图②中阴影部分的面积.
方法①(m-n)2
方法②(m+n)2-4mn
(3)观察图②,写出(m+n)2,(m-n)2,mn这三个代数式之间的等量关系:(m-n)2=(m+n)2-4mn,
故答案为:m-n;(m-n)2,(m+n)2-4mn;(m-n)2=(m+n)2-4mn;
(4)(m-n)2=(m+n)2-4mn=52-4×4=9,
m-n=3.
点评 本题考查了完全平方公式,利用(m-n)2=(m+n)2-4mn是解题关键.

练习册系列答案
相关题目
12.某股民上周五天进某公司股票2000股,每股14.8元,如表为本周内每日该股票的涨跌情况(单位:元)已知该股民买进股票时付了成交额1.5‰的手续费,卖出时付成交额1.5‰的手续费和1‰的交易税.如果他在星期五收盘前将全部股票卖出,计算一下他的收益情况.
| 星期 | 一 | 二 | 三 | 四 | 五 |
| 每股涨跌 | +1 | +1.2 | -1 | +2 | -1 |
14.一个等腰三角形的两边长分别是3和7,则它的周长为( )
| A. | 13 | B. | 15 | C. | 17 | D. | 13或17 |
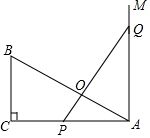 如图,已知△ABC是直角三角形,∠C=90°,AC=10cm,BC=5cm,射线AM⊥AC,点P在AC上运动(不与点A,C重合),点Q在AM上运动(不与点A重合),且始终保持PQ=AB.
如图,已知△ABC是直角三角形,∠C=90°,AC=10cm,BC=5cm,射线AM⊥AC,点P在AC上运动(不与点A,C重合),点Q在AM上运动(不与点A重合),且始终保持PQ=AB.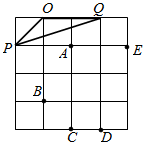 如图,△OPQ在边长为1个单位的方格纸中,它们的顶点在小正方形顶点位置,点A,B,C,D,E也是小正方形的顶点,从点A,B,C,D,E中选取三个点所构成的三角形与△OPQ相似,那么这个三角形是△CDB.
如图,△OPQ在边长为1个单位的方格纸中,它们的顶点在小正方形顶点位置,点A,B,C,D,E也是小正方形的顶点,从点A,B,C,D,E中选取三个点所构成的三角形与△OPQ相似,那么这个三角形是△CDB.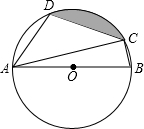 如图,四边形ABCD是⊙O的内接四边形,AB是⊙O的直径,∠D=108°,连接AC.
如图,四边形ABCD是⊙O的内接四边形,AB是⊙O的直径,∠D=108°,连接AC.