题目内容
15.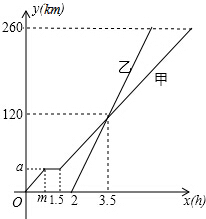 甲、乙两车从A地驶向B地,并以各自的速度匀速行驶,甲车比乙车早行驶2h,并且甲车途中休息了0.5h,如图是甲乙两车行驶的距离y(km)与时间x(h)的函数图象.则下列结论:
甲、乙两车从A地驶向B地,并以各自的速度匀速行驶,甲车比乙车早行驶2h,并且甲车途中休息了0.5h,如图是甲乙两车行驶的距离y(km)与时间x(h)的函数图象.则下列结论:(1)a=40,m=1;
(2)乙的速度是80km/h;
(3)甲比乙迟$\frac{7}{4}$h到达B地;
(4)乙车行驶$\frac{9}{4}$小时或$\frac{19}{4}$小时,两车恰好相距50km.
正确的个数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 (1)先由函数图象中的信息求出m的值,再根据“路程÷时间=速度”求出甲的速度,并求出a的值;
(2)根据函数图象可得乙车行驶3.5-2=1小时后的路程为120km进行计算;
(3)先根据图形判断甲、乙两车中先到达B地的是乙车,再把y=260代入y=40x-20求得甲车到达B地的时间,再求出乙车行驶260km需要260÷80=3.25h,即可得到结论;
(4)根据甲、乙两车行驶的路程y与时间x之间的解析式,由解析式之间的关系建立方程求出其解即可.
解答 解:(1)由题意,得m=1.5-0.5=1.
120÷(3.5-0.5)=40(km/h),则a=40,故(1)正确;
(2)120÷(3.5-2)=80km/h(千米/小时),故(2)正确;
(3)设甲车休息之后行驶路程y(km)与时间x(h)的函数关系式为y=kx+b,由题意,得
$\left\{\begin{array}{l}{40=1.5k+b}\\{120=3.5k+b}\end{array}\right.$
解得:$\left\{\begin{array}{l}{k=40}\\{b=-20}\end{array}\right.$
∴y=40x-20,
根据图形得知:甲、乙两车中先到达B地的是乙车,
把y=260代入y=40x-20得,x=7,
∵乙车的行驶速度:80km/h,
∴乙车的行驶260km需要260÷80=3.25h,
∴7-(2+3.25)=$\frac{7}{4}$h,
∴甲比乙迟$\frac{7}{4}$h到达B地,故(3)正确;
(4)当1.5<x≤7时,y=40x-20.
设乙车行驶的路程y与时间x之间的解析式为y=k'x+b',由题意得
$\left\{\begin{array}{l}{0=2k′+b′}\\{120=3.5k′+b′}\end{array}\right.$
解得:$\left\{\begin{array}{l}{k′=80}\\{b′=-160}\end{array}\right.$
∴y=80x-160.
当40x-20-50=80x-160时,
解得:x=$\frac{9}{4}$.
当40x-20+50=80x-160时,
解得:x=$\frac{19}{4}$.
∴$\frac{9}{4}$-2=$\frac{1}{4}$,$\frac{19}{4}$-2=$\frac{11}{4}$.
所以乙车行驶小时$\frac{1}{4}$或$\frac{11}{4}$小时,两车恰好相距50km,故(4)错误.
故选(C)
点评 本题主要考查了一次函数的应用,解决问题的关键是从图形中获得必要的信息进行计算,运用待定系数法求一次函数的解析式.解答此类试题时,需要掌握建立函数模型的方法以及采用分段函数解决问题的思想.

| A. | 1.2×10-7米 | B. | 1.2×10-8米 | C. | 1.2×10-9米 | D. | 12×10-8米 |
| A. | y=2x2-4 | B. | y=2(x-2)2 | C. | y=2x2+2 | D. | y=2(x+2)2 |
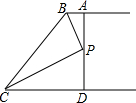 如图,AB∥CD,BP和CP分别平分∠ABC和∠DCB,AD过点P,且与AB垂直.若AD=8,则点P到BC的距离是( )
如图,AB∥CD,BP和CP分别平分∠ABC和∠DCB,AD过点P,且与AB垂直.若AD=8,则点P到BC的距离是( )
 如图,点A、B是双曲线y=$\frac{6}{x}$上的点,分别过点A、B作x轴和y轴的垂线段,若图中阴影部分的面积为2,则两个空白矩形面积的和为8.
如图,点A、B是双曲线y=$\frac{6}{x}$上的点,分别过点A、B作x轴和y轴的垂线段,若图中阴影部分的面积为2,则两个空白矩形面积的和为8.