题目内容
17.已知△ABC是等腰直角三角形,AC=BC=2,D是边AB上一动点(A、B两点除外),将△CAD绕点C按逆时针方向旋转角α得到△CEF,其中点E是点A的对应点,点F是点D的对应点.
(1)如图1,当α=90°时,G是边AB上一点,且BG=AD,连接GF.求证:GF∥AC;
(2)如图2,当90°≤α≤180°时,AE与DF相交于点M.
①当点M与点C、D不重合时,连接CM,求∠CMD的度数;
②设D为边AB的中点,当α从90°变化到180°时,求点M运动的路径长.
分析 (1)欲证明GF∥AC,只要证明∠A=∠FGB即可解决问题.
(2)①先证明A、D、M、C四点共圆,得到∠CMF=∠CAD=45°,即可解决问题.
②利用①的结论可知,点M在以AC为直径的⊙O上,运动路径是弧CD,利用弧长公式即可解决问题.
解答 解:(1)如图1中, ∵CA=CB,∠ACB=90°,
∵CA=CB,∠ACB=90°,
∴∠A=∠ABC=45°,
∵△CEF是由△CAD旋转逆时针α得到,α=90°,
∴CB与CE重合,
∴∠CBE=∠A=45°,
∴∠ABF=∠ABC+∠CBF=90°,
∵BG=AD=BF,
∴∠BGF=∠BFG=45°,
∴∠A=∠BGF=45°,
∴GF∥AC.
(2)①如图2中,∵CA=CE,CD=CF,
∴∠CAE=∠CEA,∠CDF=∠CFD,
∵∠ACD=∠ECF,
∴∠ACE=∠DCF,
∵2∠CAE+∠ACE=180°,2∠CDF+∠DCF=180°,
∴∠CAE=∠CDF,
∴A、D、M、C四点共圆,
∴∠CMF=∠CAD=45°,
∴∠CMD=180°-∠CMF=135°.
(补充:不用四点共圆的方法:由△OAC∽△ODM,推出△AOD∽△COM,推出∠OCM=∠OAD,即可证明∠CMF=∠CDM+∠DCM=∠CAO+∠OAD=∠CAD=45°)
②如图3中,O是AC中点,连接OD、CM. ∵AD=DB,CA=CB,
∵AD=DB,CA=CB,
∴CD⊥AB,
∴∠ADC=90°,
由①可知A、D、M、C四点共圆,
∴当α从90°变化到180°时,
点M在以AC为直径的⊙O上,运动路径是弧CD,
∵OA=OC,CD=DA,
∴DO⊥AC,
∴∠DOC=90°,
∴$\widehat{CD}$的长=$\frac{90π•1}{180}$=$\frac{π}{2}$.
∴当α从90°变化到180°时,点M运动的路径长为$\frac{π}{2}$.
点评 本题考查几何变换综合题、等腰直角三角形的性质、平行线的判定和性质、弧长公式、四点共圆等知识,解题的关键是发现A、D、M、C四点共圆,最后一个问题的关键,正确探究出点M的运动路径,记住弧长公式,属于中考压轴题.

 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案| A. | 0.845×104 | B. | 8.45×103 | C. | 8.45×104 | D. | 84.5×102 |
| A. |  | B. |  | C. |  | D. |  |
| A. | y=2x2-4 | B. | y=2(x-2)2 | C. | y=2x2+2 | D. | y=2(x+2)2 |
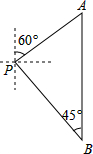 如图,小明从P点出发,沿北偏东60°方向行驶到达A处,接着向正南方向行驶100($\sqrt{3}$+1)米到达B处.在B处观测到出发时所在的P处在北偏西45°方向上,P,A两处相距多少米?
如图,小明从P点出发,沿北偏东60°方向行驶到达A处,接着向正南方向行驶100($\sqrt{3}$+1)米到达B处.在B处观测到出发时所在的P处在北偏西45°方向上,P,A两处相距多少米?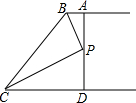 如图,AB∥CD,BP和CP分别平分∠ABC和∠DCB,AD过点P,且与AB垂直.若AD=8,则点P到BC的距离是( )
如图,AB∥CD,BP和CP分别平分∠ABC和∠DCB,AD过点P,且与AB垂直.若AD=8,则点P到BC的距离是( )