题目内容
8.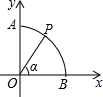 如图,以圆O为圆心,半径为1的弧交坐标轴于A,B两点,P是$\widehat{AB}$上一点(不与A,B重合),连接OP,设∠POB=α,则点P的坐标是( )
如图,以圆O为圆心,半径为1的弧交坐标轴于A,B两点,P是$\widehat{AB}$上一点(不与A,B重合),连接OP,设∠POB=α,则点P的坐标是( )| A. | (sinα,sinα) | B. | (cosα,cosα) | C. | (cosα,sinα) | D. | (sinα,cosα) |
分析 过P作PQ⊥OB,交OB于点Q,在直角三角形OPQ中,利用锐角三角函数定义表示出OQ与PQ,即可确定出P的坐标.
解答 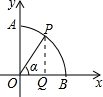 解:过P作PQ⊥OB,交OB于点Q,
解:过P作PQ⊥OB,交OB于点Q,
在Rt△OPQ中,OP=1,∠POQ=α,
∴sinα=$\frac{PQ}{OP}$,cosα=$\frac{OQ}{OP}$,即PQ=sinα,OQ=cosα,
则P的坐标为(cosα,sinα),
故选C.
点评 此题考查了解直角三角形,以及坐标与图形性质,熟练掌握锐角三角函数定义是解本题的关键.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案
相关题目
18.长春市地铁1号线预计今年9月份通车,线路总长约为18500m.数据18500用科学记数法表示是( )
| A. | 1.85×105 | B. | 1.85×104 | C. | 0.185×105 | D. | 18.5×103 |
3.下列算式中,结果等于a6的是( )
| A. | a4+a2 | B. | a2+a2+a2 | C. | a2•a3 | D. | a2•a2•a2 |
17.如图1表示同一时刻的韩国首尔时间和北京时间,两地时差为整数.
(1)设北京时间为x(时),首尔时间为y(时),就0≤x≤12,求y关于x的函数表达式,并填写下表(同一时刻的两地时间).
(2)如图2表示同一时刻的英国伦敦时间(夏时制)和北京时间,两地时差为整数.如果现在伦敦(夏时制)时间为7:30,那么此时韩国首尔时间是多少?

(1)设北京时间为x(时),首尔时间为y(时),就0≤x≤12,求y关于x的函数表达式,并填写下表(同一时刻的两地时间).
| 北京时间 | 7:30 | 11:15 | 2:50 |
| 首尔时间 | 8:30 | 12:15 | 3:50 |

18.下列一元二次方程没有实数根的是( )
| A. | x2+2x+1=0 | B. | x2+x+2=0 | C. | x2-1=0 | D. | x2-2x-1=0 |
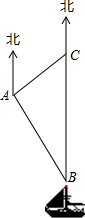 南沙群岛是我国固有领土,现在我南海渔民要在南沙某海岛附近进行捕鱼作业,当渔船航行至B处时,测得该岛位于正北方向20(1+$\sqrt{3}$)海里的C处,为了防止某国海巡警干扰,就请求我A处的渔监船前往C处护航,已知C位于A处的北偏东45°方向上,A位于B的北偏西30°的方向上,求A、C之间的距离.
南沙群岛是我国固有领土,现在我南海渔民要在南沙某海岛附近进行捕鱼作业,当渔船航行至B处时,测得该岛位于正北方向20(1+$\sqrt{3}$)海里的C处,为了防止某国海巡警干扰,就请求我A处的渔监船前往C处护航,已知C位于A处的北偏东45°方向上,A位于B的北偏西30°的方向上,求A、C之间的距离. 如图,一个由4条线段构成的“鱼”形图案,其中∠1=50°,∠2=50°,∠3=130°,找出图中的平行线,并说明理由.
如图,一个由4条线段构成的“鱼”形图案,其中∠1=50°,∠2=50°,∠3=130°,找出图中的平行线,并说明理由. 如图,AB∥DE,∠C=20°,∠B:∠D=4:3,则∠BOE=100度.
如图,AB∥DE,∠C=20°,∠B:∠D=4:3,则∠BOE=100度.