题目内容
9.能说明命题“对于任何实数a,|a|>-a”是假命题的一个反例可以是( )| A. | a=-2 | B. | a=$\frac{1}{3}$ | C. | a=1 | D. | a=$\sqrt{2}$ |
分析 反例就是符合已知条件但不满足结论的例子.可据此判断出正确的选项.
解答 解:说明命题“对于任何实数a,|a|>-a”是假命题的一个反例可以是a=-2,
故选A.
点评 本题考查了命题与定理:判断一件事情的语句,叫做命题.许多命题都是由题设和结论两部分组成,题设是已知事项,结论是由已知事项推出的事项,一个命题可以写成“如果…那么…”形式. 有些命题的正确性是用推理证实的,这样的真命题叫做定理. 任何一个命题非真即假.要说明一个命题的正确性,一般需要推理、论证,而判断一个命题是假命题,只需举出一个反例即可.

练习册系列答案
相关题目
17.如图1表示同一时刻的韩国首尔时间和北京时间,两地时差为整数.
(1)设北京时间为x(时),首尔时间为y(时),就0≤x≤12,求y关于x的函数表达式,并填写下表(同一时刻的两地时间).
(2)如图2表示同一时刻的英国伦敦时间(夏时制)和北京时间,两地时差为整数.如果现在伦敦(夏时制)时间为7:30,那么此时韩国首尔时间是多少?

(1)设北京时间为x(时),首尔时间为y(时),就0≤x≤12,求y关于x的函数表达式,并填写下表(同一时刻的两地时间).
| 北京时间 | 7:30 | 11:15 | 2:50 |
| 首尔时间 | 8:30 | 12:15 | 3:50 |

4.使二次根式$\sqrt{x-1}$有意义的x的取值范围是( )
| A. | x≠1 | B. | x>1 | C. | x≤1 | D. | x≥1 |
1.下列分式中,最简分式是( )
| A. | $\frac{{x}^{2}-1}{{x}^{2}+1}$ | B. | $\frac{x+1}{{x}^{2}-1}$ | ||
| C. | $\frac{{x}^{2}-2xy+{y}^{2}}{{x}^{2}-xy}$ | D. | $\frac{{x}^{2}-36}{2x+12}$ |
18.下列一元二次方程没有实数根的是( )
| A. | x2+2x+1=0 | B. | x2+x+2=0 | C. | x2-1=0 | D. | x2-2x-1=0 |
19.图(一)、图(二)分别为甲、乙两班学生参加投篮测验的投进球数直方图.若甲、乙两班学生的投进球数的众数分别为a、b;中位数分别为c、d,则下列关于a、b、c、d的大小关系,何者正确?( )

| A. | a>b,c>d | B. | a>b,c<d | C. | a<b,c>d | D. | a<b,c<d |
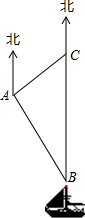 南沙群岛是我国固有领土,现在我南海渔民要在南沙某海岛附近进行捕鱼作业,当渔船航行至B处时,测得该岛位于正北方向20(1+$\sqrt{3}$)海里的C处,为了防止某国海巡警干扰,就请求我A处的渔监船前往C处护航,已知C位于A处的北偏东45°方向上,A位于B的北偏西30°的方向上,求A、C之间的距离.
南沙群岛是我国固有领土,现在我南海渔民要在南沙某海岛附近进行捕鱼作业,当渔船航行至B处时,测得该岛位于正北方向20(1+$\sqrt{3}$)海里的C处,为了防止某国海巡警干扰,就请求我A处的渔监船前往C处护航,已知C位于A处的北偏东45°方向上,A位于B的北偏西30°的方向上,求A、C之间的距离. 如图,AB∥DE,∠C=20°,∠B:∠D=4:3,则∠BOE=100度.
如图,AB∥DE,∠C=20°,∠B:∠D=4:3,则∠BOE=100度.