题目内容
6.抛物线y=2x2-2$\sqrt{2}$x+1与坐标轴的交点个数是( )| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
分析 对于抛物线解析式,分别令x=0与y=0求出对应y与x的值,即可确定出抛物线与坐标轴的交点个数.
解答 解:抛物线y=2x2-2$\sqrt{2}$x+1,显然抛物线与y轴有一个交点,
令y=0,得到2x2-2$\sqrt{2}$x+1=0,
∵△=8-8=0,
∴抛物线与x轴有一个交点,
则抛物线与坐标轴的交点个数是2,
故选C
点评 此题考查了抛物线与坐标轴的交点,抛物线解析式中令一个未知数为0,求出另一个未知数的值,确定出抛物线与坐标轴交点.

练习册系列答案
相关题目
17.如图1表示同一时刻的韩国首尔时间和北京时间,两地时差为整数.
(1)设北京时间为x(时),首尔时间为y(时),就0≤x≤12,求y关于x的函数表达式,并填写下表(同一时刻的两地时间).
(2)如图2表示同一时刻的英国伦敦时间(夏时制)和北京时间,两地时差为整数.如果现在伦敦(夏时制)时间为7:30,那么此时韩国首尔时间是多少?

(1)设北京时间为x(时),首尔时间为y(时),就0≤x≤12,求y关于x的函数表达式,并填写下表(同一时刻的两地时间).
| 北京时间 | 7:30 | 11:15 | 2:50 |
| 首尔时间 | 8:30 | 12:15 | 3:50 |

1.下列分式中,最简分式是( )
| A. | $\frac{{x}^{2}-1}{{x}^{2}+1}$ | B. | $\frac{x+1}{{x}^{2}-1}$ | ||
| C. | $\frac{{x}^{2}-2xy+{y}^{2}}{{x}^{2}-xy}$ | D. | $\frac{{x}^{2}-36}{2x+12}$ |
18.下列一元二次方程没有实数根的是( )
| A. | x2+2x+1=0 | B. | x2+x+2=0 | C. | x2-1=0 | D. | x2-2x-1=0 |
15. 《九章算术》是我国古代内容极为丰富的数学名著,书中有下列问题“今有勾八步,股十五步,问勾中容圆径几何?”其意思是:“今有直角三角形,勾(短直角边)长为8步,股(长直角边)长为15步,问该直角三角形能容纳的圆形(内切圆)直径是多少?”( )
《九章算术》是我国古代内容极为丰富的数学名著,书中有下列问题“今有勾八步,股十五步,问勾中容圆径几何?”其意思是:“今有直角三角形,勾(短直角边)长为8步,股(长直角边)长为15步,问该直角三角形能容纳的圆形(内切圆)直径是多少?”( )
 《九章算术》是我国古代内容极为丰富的数学名著,书中有下列问题“今有勾八步,股十五步,问勾中容圆径几何?”其意思是:“今有直角三角形,勾(短直角边)长为8步,股(长直角边)长为15步,问该直角三角形能容纳的圆形(内切圆)直径是多少?”( )
《九章算术》是我国古代内容极为丰富的数学名著,书中有下列问题“今有勾八步,股十五步,问勾中容圆径几何?”其意思是:“今有直角三角形,勾(短直角边)长为8步,股(长直角边)长为15步,问该直角三角形能容纳的圆形(内切圆)直径是多少?”( )| A. | 3步 | B. | 5步 | C. | 6步 | D. | 8步 |
16.若二次根式$\sqrt{a-2}$有意义,则a的取值范围是( )
| A. | a≥2 | B. | a≤2 | C. | a>2 | D. | a≠2 |
 如图,一个由4条线段构成的“鱼”形图案,其中∠1=50°,∠2=50°,∠3=130°,找出图中的平行线,并说明理由.
如图,一个由4条线段构成的“鱼”形图案,其中∠1=50°,∠2=50°,∠3=130°,找出图中的平行线,并说明理由.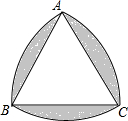 如图,△ABC是等边三角形,AB=2,分别以A,B,C为圆心,以2为半径作弧,则图中阴影部分的面积是2π-3$\sqrt{3}$.
如图,△ABC是等边三角形,AB=2,分别以A,B,C为圆心,以2为半径作弧,则图中阴影部分的面积是2π-3$\sqrt{3}$.