题目内容
7．判断2$\sqrt{11}$-1之值介于下列哪两个整数之间？（ ）| A． | 3，4 | B． | 4，5 | C． | 5，6 | D． | 6，7 |
分析 由$\sqrt{36}$＜2$\sqrt{11}$＜$\sqrt{49}$即6＜2$\sqrt{11}$＜7，由不等式性质可得2$\sqrt{11}$-1的范围可得答案．
解答 解：∵2$\sqrt{11}$=$\sqrt{44}$，且$\sqrt{36}$＜$\sqrt{44}$＜$\sqrt{49}$，即6＜2$\sqrt{11}$＜7，
∴5＜2$\sqrt{11}$-1＜6，
故选：C．
点评 本题考查了估算无理数大小的知识，注意夹逼法的运用是解题关键．
练习册系列答案
相关题目
17．如图1表示同一时刻的韩国首尔时间和北京时间，两地时差为整数．
（1）设北京时间为x（时），首尔时间为y（时），就0≤x≤12，求y关于x的函数表达式，并填写下表（同一时刻的两地时间）．
（2）如图2表示同一时刻的英国伦敦时间（夏时制）和北京时间，两地时差为整数．如果现在伦敦（夏时制）时间为7：30，那么此时韩国首尔时间是多少？
（1）设北京时间为x（时），首尔时间为y（时），就0≤x≤12，求y关于x的函数表达式，并填写下表（同一时刻的两地时间）．
| 北京时间 | 7：30 | 11：15 | 2：50 |
| 首尔时间 | 8：30 | 12：15 | 3：50 |
18．下列一元二次方程没有实数根的是（ ）
| A． | x2+2x+1=0 | B． | x2+x+2=0 | C． | x2-1=0 | D． | x2-2x-1=0 |
15．
《九章算术》是我国古代内容极为丰富的数学名著，书中有下列问题“今有勾八步，股十五步，问勾中容圆径几何？”其意思是：“今有直角三角形，勾（短直角边）长为8步，股（长直角边）长为15步，问该直角三角形能容纳的圆形（内切圆）直径是多少？”（ ）
《九章算术》是我国古代内容极为丰富的数学名著，书中有下列问题“今有勾八步，股十五步，问勾中容圆径几何？”其意思是：“今有直角三角形，勾（短直角边）长为8步，股（长直角边）长为15步，问该直角三角形能容纳的圆形（内切圆）直径是多少？”（ ）| A． | 3步 | B． | 5步 | C． | 6步 | D． | 8步 |
2．某中学组织学生到商场参加社会实践活动，他们参与了某种品牌运动鞋的销售工作，已知该运动鞋每双的进价为120元，为寻求合适的销售价格进行了4天的试销，试销情况如表所示：
（1）观察表中数据，x，y满足什么函数关系？请求出这个函数关系式；
（2）若商场计划每天的销售利润为3000元，则其单价应定为多少元？
| 第1天 | 第2天 | 第3天 | 第4天 | |
| 售价x（元/双） | 150 | 200 | 250 | 300 |
| 销售量y（双） | 40 | 30 | 24 | 20 |
（2）若商场计划每天的销售利润为3000元，则其单价应定为多少元？
12．
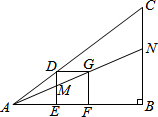如图的△ABC中有一正方形DEFG，其中D在AC上，E、F在AB上，直线AG分别交DE、BC于M、N两点．若∠B=90°，AB=4，BC=3，EF=1，则BN的长度为何？（ ）
如图的△ABC中有一正方形DEFG，其中D在AC上，E、F在AB上，直线AG分别交DE、BC于M、N两点．若∠B=90°，AB=4，BC=3，EF=1，则BN的长度为何？（ ）| A． | $\frac{4}{3}$ | B． | $\frac{3}{2}$ | C． | $\frac{8}{5}$ | D． | $\frac{12}{7}$ |
19．图（一）、图（二）分别为甲、乙两班学生参加投篮测验的投进球数直方图．若甲、乙两班学生的投进球数的众数分别为a、b；中位数分别为c、d，则下列关于a、b、c、d的大小关系，何者正确？（ ）
| A． | a＞b，c＞d | B． | a＞b，c＜d | C． | a＜b，c＞d | D． | a＜b，c＜d |
16．若二次根式$\sqrt{a-2}$有意义，则a的取值范围是（ ）
| A． | a≥2 | B． | a≤2 | C． | a＞2 | D． | a≠2 |
17．△ABC与△DEF的相似比为1：4，则△ABC与△DEF的周长比为（ ）
| A． | 1：2 | B． | 1：3 | C． | 1：4 | D． | 1：16 |