题目内容
7.若正多边形的一个内角是120°,则这个正多边形的边数为( )| A. | 8 | B. | 7 | C. | 6 | D. | 5 |
分析 多边形的内角和可以表示成(n-2)•180°,因为所给多边形的每个内角均相等,故又可表示成120°n,列方程可求解.此题还可以由已知条件,求出这个多边形的外角,再利用多边形的外角和定理求解.
解答 解:设所求正n边形边数为n,
则120°n=(n-2)•180°,
解得n=6,
故选C.
点评 本题考查根据多边形的内角和计算公式求多边形的边数,解答时要会根据公式进行正确运算是解答此题的关键.

练习册系列答案
相关题目
12. 在?ABCD中,过点D作对DE⊥AB于点E,点F在边CD上,CF=AE,连结AF,BF.
在?ABCD中,过点D作对DE⊥AB于点E,点F在边CD上,CF=AE,连结AF,BF.
(1)求证:四边形BFDE是矩形.
(2)若CF=6,BF=8,DF=10,求证:AF是∠DAB的角平分线.
 在?ABCD中,过点D作对DE⊥AB于点E,点F在边CD上,CF=AE,连结AF,BF.
在?ABCD中,过点D作对DE⊥AB于点E,点F在边CD上,CF=AE,连结AF,BF.(1)求证:四边形BFDE是矩形.
(2)若CF=6,BF=8,DF=10,求证:AF是∠DAB的角平分线.
16.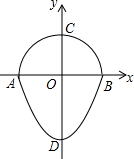 如图,是一个半圆和抛物线的一部分围成的“鸭梨”,已知点A、B、C、D分别是“鸭梨”与坐标轴的交点,AB是半圆的直径,抛物线的解析式为y=2x2-2,则图中CD的长为( )
如图,是一个半圆和抛物线的一部分围成的“鸭梨”,已知点A、B、C、D分别是“鸭梨”与坐标轴的交点,AB是半圆的直径,抛物线的解析式为y=2x2-2,则图中CD的长为( )
 如图,是一个半圆和抛物线的一部分围成的“鸭梨”,已知点A、B、C、D分别是“鸭梨”与坐标轴的交点,AB是半圆的直径,抛物线的解析式为y=2x2-2,则图中CD的长为( )
如图,是一个半圆和抛物线的一部分围成的“鸭梨”,已知点A、B、C、D分别是“鸭梨”与坐标轴的交点,AB是半圆的直径,抛物线的解析式为y=2x2-2,则图中CD的长为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
17.下列分式方程有解的是( )
| A. | $\frac{1}{2x-3}$=0 | B. | $\frac{{x}^{2}+1}{x}$=0 | C. | $\frac{2x}{x-1}=\frac{x+1}{x-1}$ | D. | $\frac{1}{x-1}=1$ |
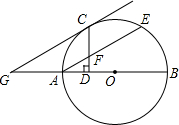 如图,AB是⊙O的直径,AE是弦,C是劣弧AE的中点,过C作CD⊥AB于D,过C作CG∥AE交BA的延长线于点G.
如图,AB是⊙O的直径,AE是弦,C是劣弧AE的中点,过C作CD⊥AB于D,过C作CG∥AE交BA的延长线于点G. 已知抛物线y=ax2-4ax+3和直线y=bx-4b+3相交于一定点A.
已知抛物线y=ax2-4ax+3和直线y=bx-4b+3相交于一定点A.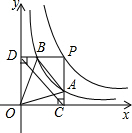 两个反比例函数y=$\frac{k}{x}$(k>1)和y=$\frac{1}{x}$在第一象限内的图象如图所示,点P在y=$\frac{k}{x}$的图象上,PC⊥x轴于点C,交y=$\frac{1}{x}$的图象于点A,PD⊥y轴于点D,交y=$\frac{1}{x}$的图象于点B,BE⊥x轴于点E,当点P在y=$\frac{k}{x}$图象上运动时,以下结论:①BA与DC始终平行;②PA与PB始终相等;③四边形PAOB的面积不会发生变化;④△OBA的面积等于四边形ACEB的面积.其中一定正确的是①③④(填序号)
两个反比例函数y=$\frac{k}{x}$(k>1)和y=$\frac{1}{x}$在第一象限内的图象如图所示,点P在y=$\frac{k}{x}$的图象上,PC⊥x轴于点C,交y=$\frac{1}{x}$的图象于点A,PD⊥y轴于点D,交y=$\frac{1}{x}$的图象于点B,BE⊥x轴于点E,当点P在y=$\frac{k}{x}$图象上运动时,以下结论:①BA与DC始终平行;②PA与PB始终相等;③四边形PAOB的面积不会发生变化;④△OBA的面积等于四边形ACEB的面积.其中一定正确的是①③④(填序号) 如图所示的图象是抛物线y=ax2+2ax+a2+2的一部分,它与x轴的一个交点A的坐标是(-3,0),则它与x轴的另一个交点的坐标为(1,0).
如图所示的图象是抛物线y=ax2+2ax+a2+2的一部分,它与x轴的一个交点A的坐标是(-3,0),则它与x轴的另一个交点的坐标为(1,0).